Chapter 11
11.1 Introduction
We have seen the integration of functions such as polynomial, rational, exponential, logarithmic and trigonometric functions. We shall now apply these in:
- finding the area under the curve and x-axis,
- finding the area between two curves,
- finding the volume of solid.
These are simple calculations but not enough when we need to find the area or volume having a complicated frame. Therefore we consider the finite integral to find area or volume of the region.
11.2 Definite Integral
If F ' (x) = f(x) when f(x) is continuous on the interval a ≤ x ≤ b, then the definite integral of f(x) on [a, b] is defined by
$$\int_a^b f(x)\,dx = F(b) - F(a)$$
where the number a and b are called the limits of integration. Here a is the lower limit and b is the upper limit.
$$\int_a^b f(x) \,dx \, \, \text{reads}$$ "the integral from x = a to x = b of f(x) with respect to x".
We write
$$F(b) - F(a) = F(x)\bigg]_a^b \, \, \text{or\,}\, \bigg[F(x)\bigg]_a^b$$ depending on whether F has one or more terms.
As an example, consider
$$\int_a^b x^3\, dx.$$ We can compute that $$\int_a^b x^3\,dx = \bigg[\frac{x^4}{4} + C\bigg]_a^b$$ $$=\left( \frac{b^4}{4}+C\right) - \left(\frac{a^4}{4}+C\right) = \frac{b^4}{4}-\frac{a^4}{4}.$$ The constant of integration C cancles out in the subtraction, so we omit it from the calculation. Thus, $$\int_a^b x^3\,dx = \frac{x^4}{4}\bigg]_a^b = \frac{b^4}{4}-\frac{a^4}{4}.$$
The Fundamental Theorem of Calculus
1. Let f be continuous on [a, b]. Then for each x ∈ [a, b],
$$\frac{d}{dx} \int_a^x f(t)\,dt = f(x).$$
2. Let F ' be continuous on [a, b]. Then for each x ∈ [a, b],
$$\int_a^x F'(t)\, dt = F(x) - F(a).$$
Rules for Definite Integration
Suppose f and g are continuous on [a, b] and k ∈ ℝ.
$$1.\, \, \int_a^b k\, f(x)\,dx = k\, \int_a^b f(x)\,dx.$$
$$2.\, \, \int_a^b [f(x)\pm g(x)]\,dx = \int_a^b \, f(x)\,dx \pm \int_a^b\,g(x)\,dx.$$
$$3. \int_a^b \, f(x)\,dx = 0.$$
$$4. \int_a^b\, f(x)\,dx = - \int_b^a\, f(x)\,dx.$$
$$5. \int_a^b\, f(x)\,dx = \int_a^c \,f(x)\,dx + \int_c^b\, f(x)\,dx \,\,\,\text{where\,} c \isin (a,b).$$
Example 1.Evaluate the following definite integrals.
$$\text{(a)\,}\, \int_{-1}^2 x^3\,dx$$ $$\text{(b)\,\,} \int_0^{\frac{\pi}{2}}\, sin\,x\,dx$$ $$\text{(c)\,}\, \int_{-1}^1\,\sqrt{x+2}\,dx$$ $$\text{(d)}\,\, \int_{\frac{\pi}{4}}^{\pi}\, |cos\, x|\, dx$$ Solution
$$\text{(a)\,}\, \int_{-1}^2 x^3\,dx$$ $$=\frac{x^4}{4}\bigg]_{-1}^2$$ $$= \frac{2^4}{4} - \frac{(-1)^4}{4}$$ $$= 3\frac{3}{4}.$$
$$\text{(b)\,\,} \int_a^{\frac{\pi}{2}}\, sin\,x\,dx$$ $$=-cos\,x\bigg]_0^{\frac{\pi}{2}}$$ $$= - cos \frac{\pi}{2} + cos\, 0$$ $$= -0+1 = 1.$$
$$\text{(c)\,}\, \int_{-1}^1\,\sqrt{x+2}\,dx$$ $$= \int_{-1}^1\, (x+2)^{\frac{1}{2}}\, dx$$ $$= \frac{2}{3} (x+2)^{\frac{1}{2}}\bigg]_{-1}^1$$ $$= \frac{2}{3} \left((3)^{\frac{3}{2}}-(1)^{\frac{3}{2}}\right)$$ $$= \frac{2}{3} (3\sqrt3-1).$$
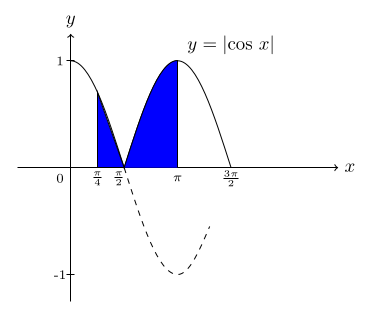
$$\text{(d)}\,\, \int_{\frac{\pi}{4}}^{\pi}\, |cos\, x|\, dx$$ $$\text{When\,}\, \frac{\pi}{4} \le x \le \frac{\pi}{2},\, |cos\,x| = cos\,x.$$ $$\text{When\,}\, \frac{\pi}{2} \le x \le \pi,\, |cos\,x| = -cos\,x.$$ $$\int_{\frac{\pi}{4}}^{\pi}\, |cos\,x|\,dx=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\, cos\,x\,dx+ \int_{\frac{\pi}{2}}^{\pi}\,(-cos\,x)\,dx$$ $$=sin\,x\bigg]_{\frac{\pi}{4}}^{\frac{\pi}{2}}\, - sin\,x \bigg]_{\frac{\pi}{2}}^{\pi}$$ $$= (sin\frac{\pi}{2}-sin\frac{\pi}{4})-(sin\,\pi - sin\frac{\pi}{2})$$ $$=2-\frac{\sqrt2}{2}.$$
Example 2.
Evaluate the integral $$\int_1^2\,x\, \sqrt{2-x}\, dx.$$ Solution
Method 1
$$\int_1^2\,x\, \sqrt{2-x}\, dx$$ Let u = 2 - x. Then du = -dx.
$$\int x\,\sqrt{2 - x}\,dx= - \int (2-u)\, \sqrt u\,du$$ $$= - \int(2u^{\frac{1}{2}}-u^{\frac{3}{2}}) du$$ $$=-\frac{4}{3} u^{\frac{3}{2}}+\frac{2}{5}u^{\frac{5}{2}}$$ $$=-\frac{4}{3}(2-x)^{\frac{3}{2}} + \frac{2}{5}(2-x)^{\frac{5}{2}}.$$ Next $$\int_1^2\,x \sqrt{2-x}\,dx = \bigg[ -\frac{4}{3}(2-x)^{\frac{3}{2}}+\frac{2}{5}(2-x)^{\frac{5}{2}}\bigg]_1^2 $$ $$= 0 - (-\frac{4}{3}+\frac{2}{5})=\frac{14}{15}.$$
Method 2
Let u = 2 - x. Then du = -dx.
Changing the variable from x to u, we get
| x | 1 → 2 |
| u | 1 → 0 |
$$\int_1^2\,x\sqrt{2-x}\,dx = - \int_1^0\, (2u^{\frac{1}{2}} - u^{\frac{3}{2}})du$$ $$= \int_0^1\, (2u^{\frac{1}{2}}-u^{\frac{3}{2}})du$$ $$= \bigg[\frac{4}{3}u^{\frac{3}{2}}-\frac{2}{5}u^{\frac{5}{2}}\bigg]_0^1 $$ $$= \frac{14}{15}.$$
Exercise 11.1
- Evaluate the following definite integrals.
- Find the integral of $$\int_0^{2\pi}\, cos\, mx\,sin\,nx\,dx$$ for (a) m = n and (b) m ≠ n.
- Evaluate the following integrals.
$$\text{(a)\,}\, \int_0^1 \frac{e^x}{e^x+1}\,dx$$ $$\text{(b)}\,\, \int_1^1\,x\sqrt{x+2}\,dx$$ $$\text{(c)}\, \, \int_0^6 \, (\frac{1}{3}x-1)^3\,dx$$ $$\text{(d)}\, \, \int_2^4\, \frac{x+5}{x^2-6x+5}\,dx$$ $$\text{(e)}\, \, \int_0^2\, e^{-x}\, cos\, 2x\,dx$$ $$\text{(f)}\, \, \int_{\frac{\pi}{8}}^{\frac{\pi}{6}}\, tan\, 2x\, dx$$
$$\text{(a)}\, \, \int_0^4\, |\sqrt{2x} - 2|\, dx$$ $$\text{(b)}\,\, \int_{-1}^1 \, |e^x-1|\,dx$$ $$\text{(c)}\, \, \int_0^{2\pi}\,|sin\,x|\,dx$$
11.3 Area between the Curve and x-axis
In this section, we discuss the area between the curve and x-axis using the definite integral. If f(x) is positive and continuous on the closed interval a ≤ x ≤ b, then the area bounded by y = f(x), the x-axis and the vertical line x = a and x = b is given by
$$\int_a^b\,f(x)\,dx.$$
Let us begin with the area enclosed between the graph and x-axis.
Example 3.
Find the area enclosed between the graph of
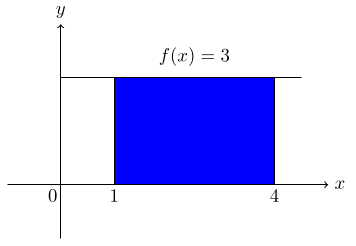
$$\text{(a)\, \,} f(x) = 3 \, \text{and\,the}\, x\text{-axis\,over\,} [1, 4],$$
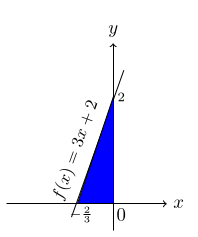
$$\text{(b)\,\,} f(x) = 3x+2 \, \text{and\,the\,}x\text{-axis\,over\,}[-\frac{2}{3}, 0].$$
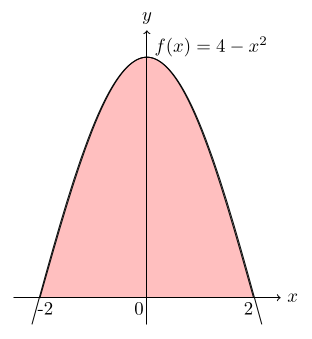
$$\text{(c)\,\,} f(x) = -x^2 + 4\, \text{and\, the\,}x\text{-axis\,over}\, [-2, 2].$$
Solution
$$\text{(a)\,\,}\, \int_1^4 \, 3\,dx = 3x\bigg]_1^4$$
$$=12 - 3 = 9 \,\text{unit}^2.$$
$$\text{(b)\,\,}\, \int_{-\frac{2}{3}}^0 \, (3x+2)\, dx = \bigg[ 3\frac{x^2}{2} + 2x\bigg]_{-\frac{2}{3}}^0$$ $$=0-\frac{3}{2}\left(-\frac{2}{3}\right)^2 - 2\left(-\frac{2}{3}\right)$$ $$=\frac{2}{3}\, \text{unit}^2.$$
$$\text{(c)\,}\, \int_{-2}^2\,(4-x^2)\,dx = \bigg[4x-\frac{x^3}{3}\bigg]_{-2}^2$$ $$= \left(8-\frac{8}{3}\right)-\left(-8+\frac{8}{3}\right)$$ $$= 10\frac{2}{3}\, \text{unit}^2.$$
Example 4.
(a) Compute the definite integral $$\int_0^{\frac{5}{2}}\, (x^2 - 2x)\,dx.$$
(b) Find the total area enclosed between the graph of f(x) = x2 - 2x and the x-axis over [0, 5⁄2].
Solution
$$\text{(a)\,\,\,}\int_0^{\frac{5}{2}}\, (x^2 - 2x)\,dx.$$ $$= \bigg[\frac{x^3}{3} - x^2\bigg]_0^{\frac{5}{2}}$$ $$= \frac{1}{3}\left(\frac{5}{2}\right)^3 - \left(\frac{5}{2}\right)^2$$ $$= -1 \frac{1}{24}.$$
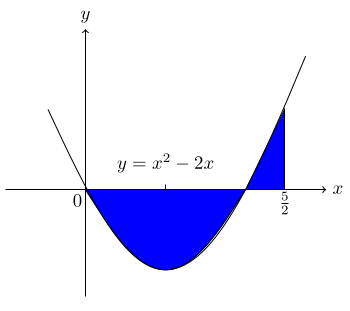
(b) For the intersection point of x-axis and the curve, f(x) = 0
$$x^2-2x=0$$ $$x(x-2)=0$$ $$x=0, 2.$$ Thus the graph of f(x) cuts x-axis at 0 and 2, we devide the domain in two intervals:
the interval [0, 2] and the interval [2, 5 ⁄2].
$$\int_0^2\, (x^2-2x)\,dx= \bigg[\frac{x^3}{3}-x^2\bigg]_0^2$$ $$=\left(\frac{8}{3}-4\right)-0=-\frac{4}{3}.$$ On [0, 2], the function f ≤ 0, so the value of integration f gives negative. $$\int_2^{\frac{5}{2}}\, (x^2-2x)\, dx = \bigg[\frac{x^3}{3}-x^2\bigg]_2^{\frac{5}{2}}$$ $$= \left(\frac{125}{24}-\frac{25}{4}\right)-\left(\frac{8}{3}-4\right)$$ $$=\frac{7}{24}.$$ On [2, 5⁄2], the function f ≥ 0, so the value of integration f gives positive.
Therefore, $$\text{Area}\, = |-\frac{4}{3}| + |\frac{7}{24}| = 1\frac{5}{8}\, \text{unit}^2.$$
Example 5.
Figure shows the graph of the function f(x) = cos x.
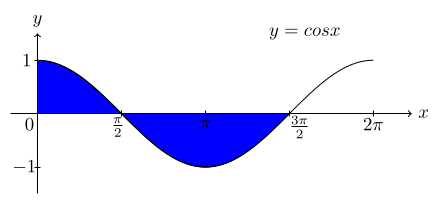
Find the area enclosed between the graph of f(x) = cos x and the lines $$\text{(a)\,}\, x=0 \, \text{and\,} x= \frac{\pi}{2}$$ $$\text{(b)\,} \, x=\frac{\pi}{2}\, \text{and\,} x=\frac{3\pi}{2}$$ $$\text{(c)\,}\, x=0\, \text{and}\, x=\frac{3\pi}{2}.$$ $$\text{(d)\, \, Find\,the\,definite\,integral}\,\, \int_0^{\frac{3\pi}{2}} \, \text{cos\,}x\,dx.$$
Solution
$$\text{(a)\,}\, \,\int_0^{\frac{\pi}{2}}\, \text{cos\,} x\,dx = \text{sin}\,\biggl]_0^{\frac{\pi}{2}}$$ $$= sin \frac{\pi}{2} - sin 0 = 1.$$ $$\text{Area\,}= 1\, \text{unit}^2.$$
$$\text{(b)\, \,} \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}}\, cos\,x\,dx= sin\, x\bigg]_{\frac{\pi}{2}}^{\frac{3\pi}{2}}$$ $$= sin \, \frac{3\pi}{2} - sin \frac{\pi}{2} = -2$$ $$\text{Area}\, = |-2| = 2\, \text{unit}^2.$$
$$\text{(c)\, \, Area\, between\, the\, graph\,} f(x)=cos\,x$$ $$\text{and\, the\, lines\,}x=0\,\text{and\,}$$ $$x=\frac{3\pi}{2}\, \text{is\,} 3\,\text{unit}^2.$$
$$\text{(d)\, \,}\, \int_0^{\frac{3\pi}{2}} \, cos\, x\,dx= sin\,x \bigg]_0^{\frac{3\pi}{2}}$$ $$= sin\frac{3\pi}{2} - sin\, 0=-1.$$
To find the area between the graph of y = f(x) and x-axis over the interval [a, b]:
Step 1 Find the intersection point(s) of the graph y = f(x) and the x-axis.
Step 2 Divide the interval [a, b] at the zeros of f.
Step 3 Integrate f over each subinterval.
Step 4 Add the absolute value of the integrals.
Example 6.
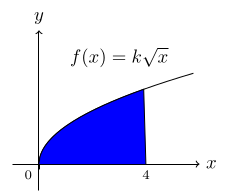
The shaded area is 16 unit2. Find the value of k.
Solution
$$\int_0^4\, k\sqrt x\,dx = \frac{2k}{3}x^{\frac{3}{2}}\bigg]_0^4$$ $$= \frac{2k}{3} \sdot 4^{\frac{3}{2}} = \frac{16k}{3}.$$ By the problem, $$\frac{16k}{3} = 16,\, \, \text{so}$$ $$k=3.$$
11.4 Area between Two Curves
In this section we consider the areas bounded by two curves.
Example 7.
Find the area between y = x2 - 2x + 2 and y = 2x - 1.
Solution
To find the x-coordinate of intersection points,
x2 - 2x + 2 = 2x - 1
x2 - 4x + 3 = 0
(x - 1)(x - 3) = 0
x = 1, 3.
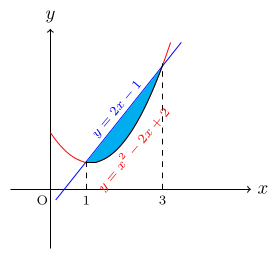
$$\text{Area\,} = \int_1^3\, [(2x-1)-(x^2-2x+2)\,]\,dx$$ $$= \int_1^3\, (-x^2 + 4x - 3)\, dx$$ $$=\bigg[-\frac{x^3}{3} + \frac{4x^2}{2} - 3x\bigg]_1^3$$ $$= 0 - (-\frac{4}{3}) = 1 \frac{1}{3}.$$
Example 8.
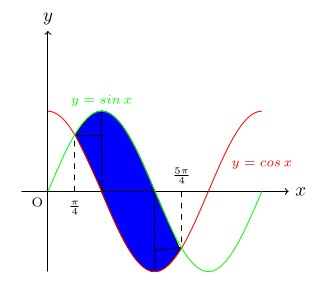
Find the area between y = sin x and y = cos x for $$\frac{\pi}{4} \le x \le \frac{5\pi}{4}$$ Solution
From the figure, we see that $$sin\,x \ge cos\,x \text{when\,} \frac{\pi}{4} \le x \le \frac{5\pi}{4}.$$ $$\text{Area\,}= \int_{\frac{\pi}{4}}^{\frac{5\pi}{4}}\, (sin\,x - cos\,x)\,dx$$ $$=\bigg[- cos\, x - sin\, x\bigg]_{\frac{\pi}{4}}^{\frac{5\pi}{4}}$$ $$=\left(-cos\, \frac{5\pi}{4}-sin\,\frac{5\pi}{4}\right)-\left(-cos\,\frac{\pi}{4} - sin\, \frac{\pi}{4}\right)$$ $$=\left(\frac{\sqrt 2}{2}+\frac{\sqrt 2}{2}\right)-\left(\frac{\sqrt 2}{2}-\frac{\sqrt 2}{2}\right)$$ $$=2\sqrt 2$$
To find the area between the graph of y = f(x) and y = g(x)
over the interval [a, b]:
Step 1 Find the intersection points of the graphs y = f(x) and g(x).
Step 2 Divide the interval [a, b] at the intersection points.
Step 3 Investigate which function is on the top at each subinterval.
Step 4 Integrate (f - g) if f is on the top, or (g - f) if g is
on the top over each subinterval.
Exercise 11.2
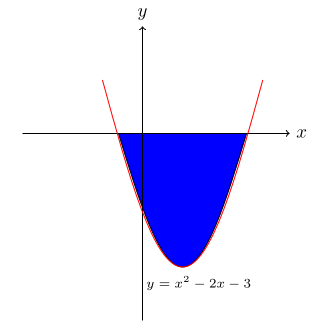
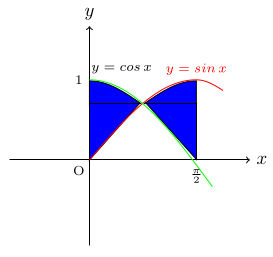
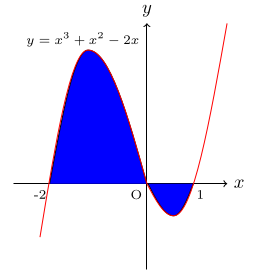
- Find the shaded areas.
- Find the area under each curve between the given x-values:
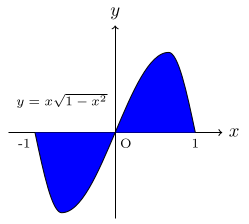
- (a) Compute $$\int_{-1}^{1} \, x\sqrt{1-x^2}\, dx.$$ (b) Find the area enclosed between the graph of $$f(x) = x\sqrt{1-x^2}$$ and the x-axis over [-1,1].
- Find the area enclosed between the graphs of y = x3 - 3x and y = x for 0 ≤ x ≤ 2.
- Find the area enclosed of the graphs of ln(3x - 2) and y = x2 - 2x + 1 for 1 ≤ x ≤ 2.
- The shaded area is 8a unit2. Find the value of a.
(a)
(b)
(c)
(d)
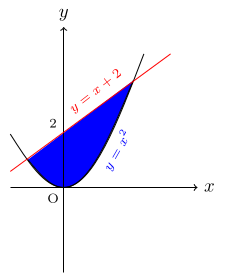
(e)
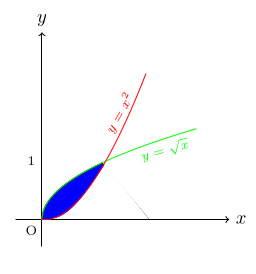
(f)
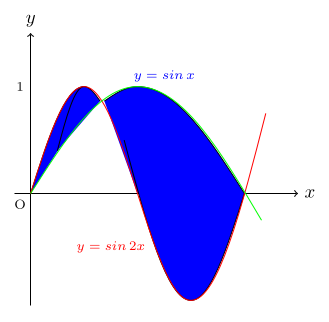
(a) f(x) = ln x from x = 1 to x = e.
(b) f(x) = 12 - 3x2 from x = -1 to x = 2.
(c) f(x) = xex2 from x = 0 to x = 1.
(d) f(x) = sin x from x = 0 to x = 3π ⁄ 2 .
(e) f(x) = (1 + cos x) sin x from x = 0 to x = π.
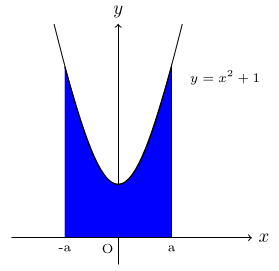
11.5 Volumes Using Cross-Sections
We studied the area between a curve and x-axis, and two curves. We now consider the volume of a particular solid by integration: the method of slicing, the disc method and the washer method.
Volume by Method of Slicing
In this section, we define volumes of solids using the areas of their cross-section. A cross-section of a solid is the plane region generated by intersecting the solid with a plane.
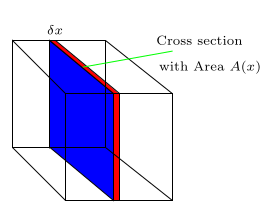
Suppose A(x) is the integrable cross-section area from x = a to x = b. We define the volume of the solid as
$$\text{Volume}\, = \int_a^b\, A(x)\, dx$$
Example 9.
A pyramid with the height of 4 m has a rectangle base shown in figure. Find the volume of the pyramid.
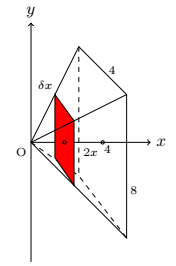
Solution
The cross-section area at x is A(x) = x2 .
$$V = \int_0^4\, A(x)\,dx$$ $$= \int_0^4\, 2x^2\, dx$$ $$= \frac{2x^3}{3}\bigg]_0^4$$ $$= \frac{128}{3}\, \text{m}^3.$$
Volume of Revolution (Disc Method)
Consider the curve y = f(x) for a ≤ x ≤ b. If the shaded part is rotated about the x-axis through 360°, a three-dimensional solid will be formed. This solid is called a solid of revolution. We can find the volume of this generated solid by definite integration.
$$\text{Volume\,of\,revolution\,}=\pi\,\int_a^b\,[f(x)]^2\,dx.$$
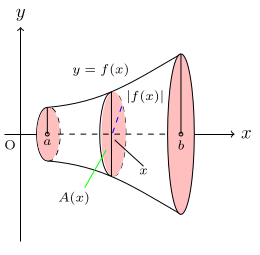
Example 10.
Find the volume of revolution formed when the curve $$\text{(a)\,\,} y=\sqrt x \, \text{for}\, 0\lt x \le 3$$ $$\text{(b)\,\,} y=x^2\, \text{for}\, 0 \lt x \lt 1$$ are rotated through 360° about the x-axis.
Solution
(a)
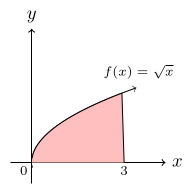
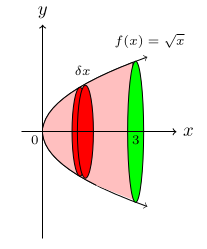
$$\text{Volume\, of\, revolution\,}= \pi\, \int_0^3 \, (\sqrt{x})^2\,dx$$ $$= \pi\, \int_0^3\, x\,dx$$ $$= \pi \frac{x^2}{2}\bigg]_0^3$$ $$= \frac{9\pi}{2}\, \text{unit}^3.$$
(b)
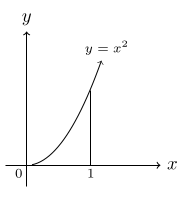
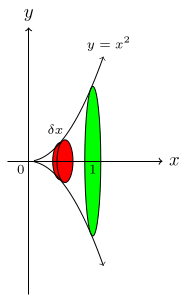
$$\text{Volume\, of\, revolution\,}= \pi\, \int_0^1 \, ({x^2})^2\,dx$$ $$= \pi\, \int_0^1\, x^4\,dx$$ $$= \pi \frac{x^5}{5}\bigg]_0^1$$ $$= \frac{\pi}{5}\, \text{unit}^3.$$
Example 11.
Find the volume of revolution formed when the curve y = sin x for π ⁄ 4 ≤ x ≤ π, is rotated through 360° about the x-axis.
Solution
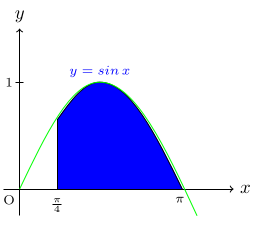
$$\text{Volume\, of\, revolution\,}= \pi\, \int_{\frac{\pi}{4}}^{\pi} \, sin2\,x\,dx$$ $$=\pi\, \int_{\frac{\pi}{4}}^{\pi}\, \frac{1-cos\,2x}{2}\,dx$$ $$= \pi\,\bigg[\frac{x}{2}-\frac{sin\,2x}{4}\bigg]_{\frac{\pi}{4}}^{\pi}$$ $$= \pi \left(\frac{\pi}{2}-\frac{sin\,2\pi}{4}\right)-\pi\left(\frac{\pi}{8}-\frac{sin\,\frac{\pi}{2}}{4}\right)$$ $$= \pi \left(\frac{\pi}{2}-0\right)-\left(\frac{\pi}{8}-\frac{1}{4}\right)$$ $$=\left(\frac{3\pi^2}{8}+\frac{\pi}{4}\right)\, \text{unit}^3.$$
Volume of Revolution (Washer Method)
If the region bounded by y = f(x) (on top) and y = g(x) and the limits x = a, x = b is revolved about the x-axis, then its volume of revolution is given by
$$\text{Volume of revolution \,}= \pi\,\int_a^b\, [(f(x))^2 - (g(x))^2]\,dx.$$
Example 12.Find the volume of revolution generated by revolving the regions between y = x2 and y = √ x about the x-axis.
Solution
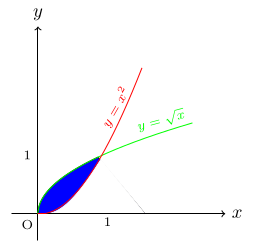
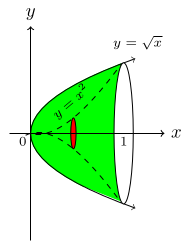
The two graphs cut x-axis at 0 and 1. the curve y = x2 and y = √ x is bounded above. $$V=\pi\, \int_0^1\, [(\sqrt x)^2 - (x^2)^2]\,dx$$ $$=\pi\, \int_0^1\, [x-x^4]\,dx$$ $$= \pi\, \bigg[\frac{x^2}{2}-\frac{x^5}{2}\bigg]_0^1$$ $$= \frac{3\pi}{10}\, \text{unit}^3.$$
To find the volume of revolution formed the graph of y = f(x), y = g(x)
rotated about x-axis:
Step 1 Find the intersection points of the graphs y = f(x) and g(x).
Step 2 Investigate which function is on the top.
Step 3 Integrate (f2 - g2) if f is on the top, or (g2 - f2)
if g is on the top on the interval.
Exercise 11.3
Find the volume of solid by using slicing method in Exercise 1-3.
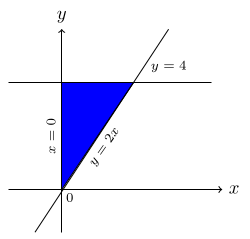
- The base of the solid is the region bounded by the graphs of y = 2x, y = 4 and x = 0. The cross-section perpendicular to the x-axis are
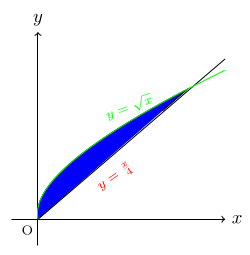
- The base of the solid is bounded by the graph of $$y=\sqrt x \, \text{and}\, y=\frac{x}{4}.$$ The cross-section perpendicular to the x-axis are
- The solid lies between the planes perpendicular to the x-axis at x = -1 and x = 1. The cross-section perpendicular to the x-axis are circular disks whose diameters run from y = -x2 + 4 and x2 + 2.
- By using the disc method, find the volume of revolution formed when the curve y = f(x) for a ≤ x ≤ b is rotated through 360° about the x-axis.
- By using the washer method, find the volume of revolution generated by revolving the regions between y = f(x) and y = g(x) for a ≤ x ≤ b about the x-axis.
(b) rectangle of perimeter 10.
(a) isosceles triangles of height 4.
(b) semicircles with diameters running across the base of solid.
$$\text{(a)\,}\, f(x) = 3x+2;\, \, \, a=\frac{1}{2}, \, \, b=4.$$ $$\text{(b)\,}\, f(x)=\sqrt{cos\,x};\, \, \, a=0, \, \, b=\frac{\pi}{2}.$$ $$\text{(c)\,}\, f(x) = \frac{1}{x-1}; \, \, \, a=3, \, \, b=5.$$ $$\text{(d)\,}\, f(x) = sin\,x\,cos\,x; \, \, \, a=0, \, \, b=\frac{\pi}{2}.$$ $$\text{(e)\,}\, f(x)= \sqrt x\, \sqrt[4]{1+x^2}; \, \, \, a=2, \, \, b=3.$$
$$\text{(a)\,}\, f(x) = x^2, \, \, g(x) = 2x;\, \, \, a=0, \, \, b=2.$$ $$\text{(b)\,}\, f(x)=tan\, x,\, \, g(x) = \frac{x}{2};\, \, \, a=0, \, \, b=\frac{\pi}{4}.$$ $$\text{(c)\,}\, f(x) = 2\sqrt x, \, \, g(x) = 2; \, \, \, a=0, \, \, b=1.$$
