Chapter 8

Logarithmic and Exponential Functions

This chapter contains logarithmic and exponential functions as a continuous study of those of logarithms and exponents of numbers from grade 10.

8.1 Logarithmic Functions

For a number b > 0, b ≠ 1, the logarithmic function y = log_b x is defined as y is a number such that x = b^y for x > 0.
The graphs of y = log₂ x and y = log_{_{¹ ⁄₂}} x are as follows.
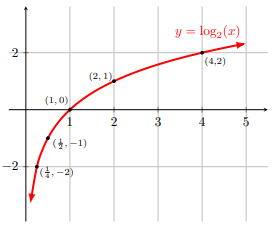
fig 8.1-1

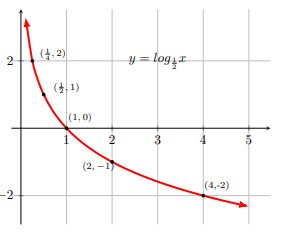
Domain of y = log_bx: x > 0
Range: ℝ
Asymptote: y-axis (x = 0)
For b > 1, y = log_bx is an increasing function that means if x₁ > x₂ then y₁ = log_bx₁ > y₂ = log_bx₂. For example, y = log₂x is an increasing function.
For 0 < b < 1, y = log_bx is a decreasing function that means if x₁ > x₂ then y₁ = log_b x₁ < y₂ = log_bx₂. For example, y = log_{_¹⁄₂} x is a decreasing function.
Since log_{¹⁄_b} x = - log_b x,
$$y = \text{log}_b\, x \xrightarrow[\text{on} \, x\text{-axis}] {\text{reflection}} \, y = \text{log}_{\tiny{\dfrac{1}{b}}}\, x $$ as the graphs of y = log₂x and y = log_¹⁄₂ x.

For b > 1, the graph of y = log_bx is vertical scaling with scale factor ¹⁄_log₂b of the graph y = log₂x.

log_b x = ^{log₂ x}⁄_{log₂ b} so that $$y = \text{log}_2\, x \xrightarrow[\text{scale factor} \, \tiny{\dfrac{1}{\text{log}_2 b}}] {\text{vertical scaling}} \, y = \text{log}_b\, x $$
For 0 < b < 1, the graph of y = log_b x is vertical scaling with scale factor ¹⁄_{log_{_¹⁄₂} b} of the graph y = ¹⁄_{log_{_¹⁄₂} x} .
$$log_b x = \frac{log_{\frac{1}{2}}x}{log_{\frac{1}{2}} b}$$ so that
$$y = \text{log}_{\tiny{\dfrac{1}{2}}}\, x \xrightarrow[\text{scale factor} \, \tiny{\dfrac{1}{\text{log}_{\tiny{\dfrac{1}{2}}} b}}] {\text{vertical scaling}} \, y = \text{log}_b\, x $$ Therefore all graphs of y = log_b x are vertical scaling of the graph of y = log₂ x or th graph of y = log_{_¹⁄₂} x. So as in y = log₂ x and y = log_{_¹⁄₂} x, we have

b > 1	0 < b < 1
y = log_b x < 0, if 0 < x < 1 y = log_b x = 0, if x = 1 y = log_b x > 0, if x > 1	y = log_b x > 0, if 0 < x < 1 y = log_b x = 0, if x = 1 y = log_b x < 0, if x > 1

Example 1.
From the graph of y = log₂ x, draw step-by-step transformation graph to get the graph of (a) y = log₂ (x - 1) + 2
(b) y = log_{_¹⁄₂} (x + 2) - 1.
Solution

$$\text{(a)}\, \, \, y = \text{log}_2 x \xrightarrow[\text{vertical translation 2 units}] {\text{horizontal translation 1 unit}} \, y = \text{log}_2\, (x - 1) + 2 $$

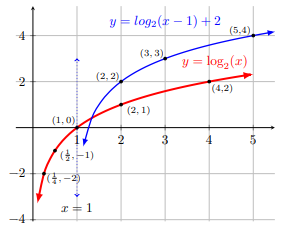
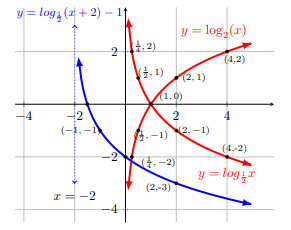
$$\text{(b)} \, \, \, y = \text{log}_2\, x \xrightarrow[\text{on}\, x\text{-axis}] {\text{reflection}} \, y $$ $$ = \text{log}_{\tiny\dfrac{1}{2}}\, x \, \xrightarrow[\text{vertical translation -1 unit}] {\text{horizontal translation -2 units}} \, y $$ $$ = \text{log}_{\tiny{\dfrac{1}{2}}} (x + 2) -1$$ fig 8.1-4

Example 2
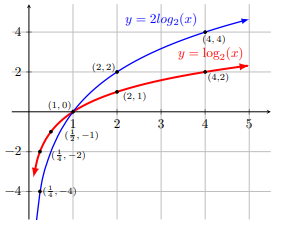
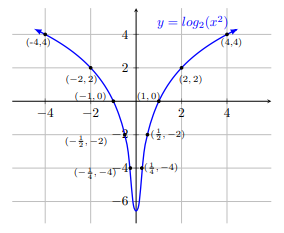
Draw the graph of y = 2 log₂ x and y = log₂ x²
Solution
The graph of y = 2 log₂ x can be drawn directly or can be drawn as the vertical scaling with scale factor 2 of the graph of y = log₂ x. Domain of y = log₂ x² is ℝ \ {0} and y = log₂ x² is an even function.
fig 8.1-5

Note: Asymptote y-axis (x = 0) fig 8.1-6

Note: Asymptote y-axis (x = 0)
Note that 2 log₂ x = log₂ x² for x > 0.
Exercise 8.1
1. Draw the graph of
(a) y = log₂(x - 2) + 1

(b) y = log₂ (x + 1) - 2

(c) y = log_{_{¹⁄ ₂}} (x + 1) + 2

(d) y = log_{_{¹⁄ ₂}} (x - 2) - 1

2. Draw the graph of
(a) y = log_{_{¹⁄ ₂}} x²

(b) y = log_{_{¹⁄ ₂}} x

3. Draw the graph of
(a) y = log₂(-x)

(b) y = log_{_{¹⁄ ₂}} (-x)

4. Draw the graph of
(a) y = log₂ |x|

(b) y = log_{_{¹⁄ ₂}} |x|

8.2 Differentiation of Logarithmic Functions

Derivative of y = log_b x

Let y = log_b x.
Let δx be a small increasement in x and δy be corresponding small increasement in y.
Then
y + δy = log_b (x + δx)
δy = log_b (x + δx) - log_b x
= log_b ^{x + δx}⁄_x
^δy⁄_δx = ¹⁄_δx log_b ^{x + δx}⁄_x
= log_b ( ^{x + δx}⁄_x ) ^{^¹⁄_δx}
= log_b (1 + ^δx⁄_x ) ^{^¹⁄_δx}

Let ^δx⁄_x = t, then ¹⁄_δx = ¹⁄_xt.
^δy⁄_δx = log_b (1 + t)^{^¹⁄_xt}
= ¹⁄_xlog_b (1 + t)^{^¹⁄_t}

When δx → 0, so t → 0. Then
$$\small{ \frac{dy}{dx} = \lim_{\delta x \rightarrow 0} \frac{\delta y}{\delta x} }$$ $$\small{ = \frac{1}{x} \lim_{t \to 0} log_b (1 + t)^{\frac{1}{t}} }$$ $$\small{ = \frac{1}{x} log_b (\lim_{t \to 0} (1 + t)^{\frac{1}{t}}) } $$
The following table shows
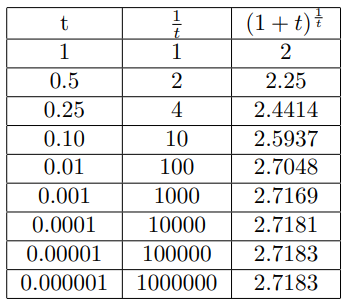
$$\small{ \lim_{t\to 0}(1 + t)^{\frac{1}{t}} = ? }$$ fig 8.2-1

The above table shows that (1 + t)^{^¹⁄_t} → 2.7183 as t → 0.
This limit value is denoted by e which is called the exponential number.
In fact, e is an irrational number.
Therefore,
^dy⁄_dx = ¹⁄_x log_b e
^d⁄_dx log_b x = ¹⁄_x log_b e

If u(x) > 0 is a function of x,

^d⁄_dx log_b u(x) = ¹⁄_u(x) ⋅ log_b e ⋅ ^d⁄_dx u(x)
Logarithm of x to the base e is called natural or Napierian Logarithm and denote log_e x = ln x.
Since
^d⁄_dx log_b x = ¹⁄_x log_b e
^d⁄_dx log_e x = ¹⁄_x log_e e
∴ ^d⁄_dx ln x = ¹⁄_x
In general
^d⁄_dx ln u(x) = ¹⁄_u(x) ⋅ ^du⁄_dx
Example 3.
Differentiate the following functions with respect to x
(a) log_₁₀ x³
(b) log_₂ x³
(c) ln x³
$$\small{ \text{(d)} \,\, \text{ln}\, \sqrt{x^2 + 5} }$$ (e) ln sin 2x
(f) ln x log₁₀ x
$$\small{ \text{(g)} \,\, \text{ln}\, \frac{x}{\sqrt{x^2 + 2} } }$$ (h) ^x²⁄ _{log₁₀ x}
Solution
(a) log_₁₀ x³

^d⁄ _dx log_₁₀ x³	=	¹⁄ _x³ log_₁₀ e ^d⁄ _dx x³
	=	¹⁄ _x³ log_₁₀ e . 3x²
	=	¹⁄ _{x . x²} . 3x² log_₁₀ e
	=	³⁄ _x log_₁₀ e .

(b) log_₂ x³

^d⁄ _dx log_₂ x³	=	¹⁄ _x³ log_₂ e ^d⁄ _dx x³
	=	¹⁄ _x³ log_₂ e . 3x²
	=	¹⁄ _{x . x²} . 3x² log_₂ e
	=	³⁄ _x. log_₂ e .

^d⁄ _dx ln x³	=	¹⁄ _x³ ^d⁄ _dx x³
	=	¹⁄ _x³ . 3x²
	=	¹⁄ _{x . x²} . 3x²
	=	³⁄ _x

$$\small{ \text{(d)} \,\, \text{ln}\, \sqrt{x^2 + 5} }$$ $$\small{ \frac{d}{dx}\, \text{ln}\, \sqrt{x^2 + 5} = \frac{1}{\sqrt{x^2 + 5}} \sdot \, \frac{d}{dx} \sqrt{x^2 + 5}}$$ $$\small{ = \frac{1}{\sqrt{x^2 + 5}} \sdot \frac{d}{dx} (x^2 + 5)^{\frac{1}{2} } } $$ $$\small{ = \frac{1}{\sqrt{x^2 + 5}} \sdot \frac{1}{2} (x^2 + 5)^{- \frac{1}{2}} \sdot \frac{d}{dx} (x^2 + 5) } $$ $$\small{ = \frac{1}{\sqrt{x^2 + 5}} \sdot \frac{1}{\cancel{2}} (x^2 + 5)^{- \frac{1}{2}} \sdot \cancel{2}x } $$ $$\small{ = \frac{1}{\sqrt{x^2 + 5}} \sdot \frac{1}{(x^2 + 5)^{\frac{1}{2} }} \sdot x } $$ $$\small{ = \frac{x}{\sqrt{x^2 + 5} \sdot \sqrt{x^2 + 5}} } $$ $$\small{ = \frac{x}{x^2 + 5} } $$
(e) ln sin 2x

^d⁄ _dx ln sin 2x	=	¹⁄ _{sin 2x}. ^d⁄ _dx sin 2x
	=	¹⁄ _{sin 2x} . cos 2x ^d⁄ _dx2x
	=	¹⁄ _{sin 2x} . 2 cos 2x
	=	^{2 cos 2x}⁄ _{sin 2x}
	=	2 cot 2x (∵ ^{cos θ}⁄ _{sin θ} = cot θ)

(f) ln x.log₁₀ x

^d⁄ _dx ln x.log₁₀ x	=	ln x ^d⁄ _dx log₁₀ x + log₁₀ x ^d⁄ _dx ln x
	=	ln x ¹⁄ _x log₁₀ e + log₁₀ x . ¹⁄ _x

$$\small{ \text{(g)} \,\, \text{ln}\, \frac{x}{\sqrt{x^2 + 2} } }$$ $$\small{ \frac{d}{dx}\, \text{ln}\, \frac{x}{\sqrt{x^2 + 2}}= \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{d}{dx} \frac{x}{\sqrt{x^2 + 2}}}$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\sqrt{x^2 + 2} \,\frac{dx}{dx} - x\, \frac{d}{dx}\, \sqrt{x^2 + 2}}{(\sqrt{x^2 + 2})^2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\sqrt{x^2 + 2} \,\frac{dx}{dx} - x\, \frac{d}{dx}\, (x^2 + 2)^{\frac{1}{2}}}{(\sqrt{x^2 + 2})^2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\sqrt{x^2 + 2} \sdot 1 - x\sdot \frac{1}{2}\, (x^2 + 2)^{- \frac{1}{2}} \sdot \frac{d}{dx} (x^2 + 2)}{x^2 + 2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\sqrt{x^2 + 2} - x\sdot \frac{1}{\cancel{2}}\, (x^2 + 2)^{- \frac{1}{2}} \sdot \cancel{2}x}{x^2 + 2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\sqrt{x^2 + 2} - \frac{x \sdot x}{(x^2 + 2)^{\frac{1}{2}} } } {x^2 + 2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\sqrt{x^2 + 2} - \frac{x^2}{\sqrt{x^2 + 2} } } {x^2 + 2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{\frac{\sqrt{x^2 + 2} \,\sdot\, \sqrt{x^2 + 2} }{\sqrt{x^2 + 2}} - \frac{x^2}{\sqrt{x^2 + 2} } } {x^2 + 2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{ \frac{x^2 + 2 - x^2}{\sqrt{x^2 + 2} } } {x^2 + 2} }$$ $$\small{ = \frac{\sqrt{x^2 + 2}}{x} \sdot \frac{ \frac{2}{\sqrt{x^2 + 2} } } {x^2 + 2} }$$ $$\small{ = \frac{\cancel{\sqrt{x^2 + 2}}}{x} \sdot \frac{ 2 } {x^2 + 2 \sdot \cancel{\sqrt{x^2 + 2}}} }$$ $$\small{= \frac{2}{x(x^2 + 2)} }$$
(h) ^x²⁄ _{log₁₀ x}

^d⁄ _dx ^x²⁄ _{log₁₀ x}	=	^{log₁₀ x. ^d⁄ _dx x² - x². ^d⁄ _dx log₁₀ x}⁄ _{(log₁₀ x)²}
	=	^{log₁₀ x . 2x - x² . ¹⁄ _x . log₁₀ e}⁄ _{(log₁₀ x)²}
	=	^{2x.log₁₀ x - x . log₁₀ e}⁄ _{(log₁₀ x)²}

Logarithmic Differentiation: The derivative of positive functions can be found by taking the natural logarithm of both sides before differentiating as in the following examples.

Example 4.
$$ \small{ \text{find} \, \frac{dy}{dx} \, \text{if} \, y = \sqrt{(x^2 + 1) (x - 1)^2} } $$ Solution
$$ \small{ y = \sqrt{(x^2 + 1) (x - 1)^2} } $$ $$ \small{ \text{ln} \, y = \text{ln} \,\sqrt{(x^2 + 1) (x - 1)^2} } $$ $$ \small{= \frac{1}{2}\, (\text{ln}\, (x^2 + 1) (x - 1)^2) } $$ $$ \small{\frac{d}{dx} \, \text{ln}\, y = \frac{d}{dx}\, (\frac{1}{2}\, (\text{ln}\, (x^2 + 1) (x - 1)^2)) } $$ $$ \small{ \frac{1}{y} \frac{dy}{dx} = \frac{1}{2}(\frac{1}{x^2 + 1} \, \sdot 2x \, + \, \frac{1}{(x - 1)^2}\sdot 2(x - 1)) } $$ $$ \small{ = \frac{x}{x^2 + 1} + \frac{2}{x - 1} }$$ $$ \small{ \frac{dy}{dx} = y(\frac{x}{x^2 + 1} + \frac{2}{x - 1}) }$$ $$ \small{ = \sqrt{(x^2 + 1) (x - 1)^2} \, (\frac{x}{x^2 + 1} + \frac{2}{x - 1}) } $$
Example 5
Find ^dy ⁄ _dx if $$\small{ y = \frac{x\,sin \,x}{\sqrt{sec\, x}}} , \, \, \, \, 0 \lt x \lt \frac{\pi}{2}. $$ Solution
$$\small{ y = \frac{x\,sin\, x}{\sqrt{sec\, x}}} , \, \, \, \, 0 \lt x \lt \frac{\pi}{2}. $$ $$\small{ \text{ln} \, y = \text{ln} (\frac{x \, sin\, x}{\sqrt{sec\, x}}) }$$ = ln x + ln sin x - ¹⁄₂ ln sec x
^d⁄_dx ln y = ^d⁄_dx(ln x + ln sin x - ¹⁄₂ ln sec x)
¹⁄_y ^dy⁄_dx = ¹⁄_x + ¹⁄_{sin x} ⋅ cos x - ¹⁄₂ ¹⁄_{sec x} ⋅ sec x ⋅ tan x
= ¹⁄_x + cot x - ¹⁄₂ tan x
^d⁄_dx = y(¹⁄_x + cot x - ¹⁄₂ tan x)
$$\small{ = \frac{x \, sin \, x}{\sqrt{sec \, x}} (\frac{1}{x} \, + \, cot \, x \, - \, \frac{1}{2} \, tan \, x) }$$ Exercise 8.2
1. Differentiate the following functions with respect to x.

(a) ln (2x² + 3)

(b) ln |x|

(c) x² log₂ x

(d) sin 3x ⋅ log₁₀ (x + 1)

$$\small{ \text{(e)}\,\, \text{ln}\, \sqrt{5x - 4}}$$
(f) ln (ln x)

2. Use logarithmic differentiation to find the derivative of y with respect to x.
$$\small{ \text{(a)}\,\, \sqrt{x(x + 1)} }$$
(b) y = x(x + 1) (x + 2)

$$\small{\text{(c)}\,\, y = \frac{x\sqrt{x^2 + 1}}{(x + 1)^{\frac{2}{3}} } }$$

8.3 Exponential Functions

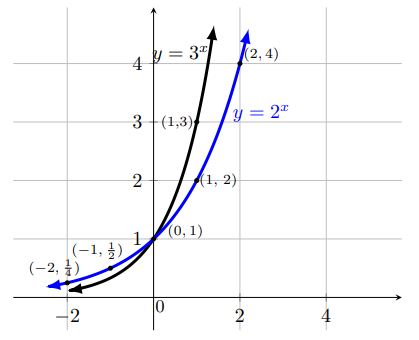
A function of the form y = b^x , where b > 0, b ≠ 1, is called an exponential function of x.
The graph y = 2^x, y = 3^x, y = 2^-x, and 3^-x are as follows.
fig 8.3-1

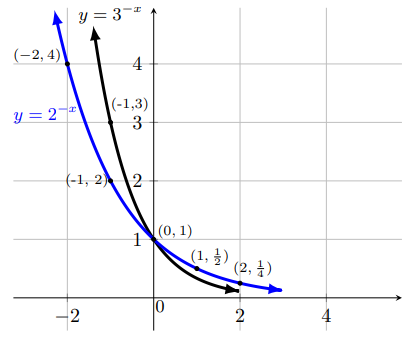
Domain of y = b^x : ℝ
Range: x > 0
Asymptote: x-axis (y = 0)

Note that y = log_bx and y = b^x are inverse of each other.
For b > 1, y = b^x is an exponential growth function as the functions
y = 2^x andy = 3^x.
For 0 < b < 1, y = b^x is an exponential decay function as the functions y = 2^-x = (¹⁄₂)^x and y = 3^-x = (¹⁄₃)^x

$$\small{y = b^x \xrightarrow[\text{on} \, y\text{-axis}] {\text{reflection}} \, y = b^{-x} }$$
From the graph of y = b^x, the graph of y = ab^x , a > 0 can be obtained as
$$\small{y = b^x \xrightarrow[\text{scale factor} \,a] {\text{vertical scaling}} \, y = ab^{x} }$$
From the graph of y = ab^x, a > 0, the graph of y = ab^{x - h} + k can be obtained as
$$\small{y = ab^x \xrightarrow[\text{vertical translation} \, k\,\text{units}] {\text{horizontal translation}\, h\, \text{units}} \, y = ab^{x - h} + k }$$ Example 6.
Draw the graph of y = 1.5 ⋅ 2^x-1 - 1 from y = 2^x , and y = -2^-(x+1) + 2 from y = -2^-x.
Solution
$$\small{y = 2^x \xrightarrow[\text{scale factor} \,1.5] {\text{vertical scaling}} \, y }$$ $$\small{ = 1.5 \sdot 2^x \xrightarrow[\text{vertical translation -1 unit}] {\text{horizontal translation 1 unit}} \, y }$$ = 1.5 ⋅ 2^x-1 - 1
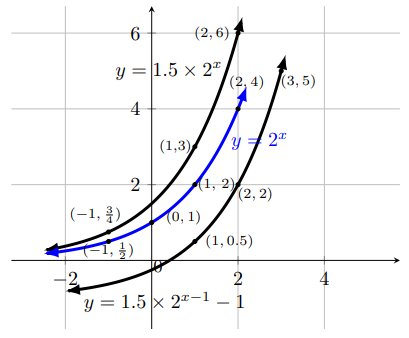
fig 8.3-3

Note: Asymptote y = -1

$$\small{y = -2^{-x} \xrightarrow[\text{2 units}] {\text{vertical translation}} \, y }$$ $$\small{ = -2^{-x} + 2 \xrightarrow[\text{-1 unit}] {\text{horizontal translation}} \, y }$$ = -2^-(x+1) + 2

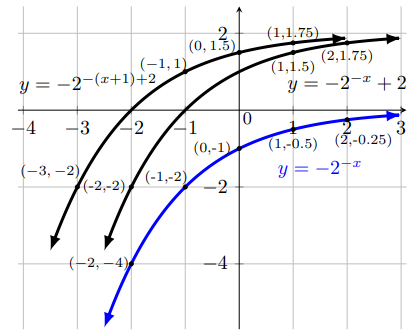
fig 8.3-4

Note: Asymptote y = 2

Example 7.
Points (0,1) and (1, b) are on the graph of y = b^x . Find the corresponding points on the graphs of y = ab^x and y = ab^{x - h} + k. What is the asymptote of y = ab^x-h + k ?
Find the range of y = ab^x-h + k if a > 0 and if a < 0.
Solutiion
$$\small{y = b^x \xrightarrow[\text{scale factor} \,a] {\text{vertical scaling}} \, y }$$ $$\small{ = ab^x \xrightarrow[\text{vertical translation}\, k \, \text{units}] {\text{horizontal translation}\, h\, \text{units}} \, y }$$ = ab^x-h + k
$$\small{(0, 1) \xrightarrow[\text{scale factor} \,a] {\text{vertical scaling}}\, (0,a) \xrightarrow[\text{vertical translation}\, k \, \text{units}] {\text{horizontal translation}}\, (h\,, a+k) }$$ $$\small{(1,b) \xrightarrow[\text{scale factor} \,a] {\text{vertical scaling}}\, (1,ab) \xrightarrow[\text{vertical translation}\, k \, \text{units}] {\text{horizontal translation}}\, (1+h\,, ab+k) }$$ Asymptote of y =b^x is y = 0 (x-axis) and asymptote of y = ab^x is also y = 0 (x-axis).
After vertical translation k units, asymptote of y = ab^x-h + k is y = k.
If k > 0, than the range of y = ab^x-h + k is {y : y > k} that means all of y above the asymptote y = k.
If a < 0, then the range of y = ab^x-h + k is {y : y < k} that means all of y below the asymptote y = k.

Exercise 8.3
1. Draw the graph of
(a) y = 2 ⋅ 3^{x + 1} - 2

(b) y = -2^x-1 + 3

2. Draw the graph of
(a) y = 2^|x|

(b) y = 2^|-x|

3. Find the y-intercept, asymptote and the range of
(a) y = 3e^x-1 + 2

(b) y = -2e^-x+1 + 3

8.4 Differentiation of Exponential Functions

Derivative of y = b^x, b > 0, b ≠ 1
y = b^x, b > 0, b ≠ 1
∴ x = log_b y

Differentiate both sides with respect to x,
1 = ¹⁄_y log_be ⋅ ^dy⁄_dx
^dy⁄_dx = y ⋅ ¹⁄_{log_b e} = b^x log_eb = b^x ln b

Therefore

^d⁄_dx b^x = b^x ln b

Since ln e = 1,

^d⁄_dx e^x = e^x

and

^d⁄_dx e^u(x) = e^u(x) ⋅ ^d⁄_dx u(x)

In general

^d⁄_dx b^u(x) = b^u(x) ⋅ ln b ⋅ ^d⁄_dx u(x)

Example 8.
Differentiate the following functions with respect to x.
(a) e^3x
(b) e^1-x²
(c) e^{sin x}
(d) x²e^3x
(e) e^2x sin 3x
(f) (e^x + e^-x)²
(g) ^{3e^2x}⁄_{1 - 2x}
Solution
(a) e^3x
^d⁄_dx e^3x = e^3x ^d⁄_dx 3x
= e^3x ⋅ 3
= 3 e^3x

(b) e^1-x²
^d⁄_dx e^1-x² = e^1-x² ^d⁄_dx (1 - x²)
= e^1-x² ⋅ (-2x)
= -2x ⋅ e^1-x²

(c) e^{sin x}
^d⁄_dx e^{sin x} = e^{sin x} ^d⁄_dx sin x
= e^{sin x} cos x
= cos x ⋅ e^{sin x}

(d) x²e^3x
^d⁄_dx x²e^3x = x² ^d⁄_dx e^3x + e^3x ^d⁄_dx x²
= x² ⋅ e^3x ^d⁄_dx 3x + e^3x ⋅ 2x
= x² ⋅ e^3x ⋅ 3 + e^3x ⋅ 2x

(e) e^2x sin 3x
^d⁄_dx e^2x sin 3x = e^2x ^d⁄_dx sin 3x + sin 3x ^d⁄_dx e^2x
= e^2x ⋅ cos 3x ^d⁄_dx 3x + sin 3x ⋅ e^2x ⋅ ^d⁄_dx 2x
= e^2x ⋅ cos 3x ⋅ 3 + sin 3x ⋅ e^2x ⋅ 2
(f) (e^x + e^-x)²
^d⁄_dx (e^x + e^-x)² = 2(e^x + e^-x). ^d⁄ _dx (e^x + e^-x)
= 2 (e^x + e^-x).( ^d⁄ _dx e^x + ^d⁄ _dx e^-x)
= 2 (e^x + e^-x).(e^x + e^-x ^d⁄ _dx -x )
= 2 (e^x + e^-x).(e^x + e^-x (-1) )
= 2 (e^x + e^-x).(e^x - e^-x)

(g) ^{3.e^2x}⁄ _1-2x
^d⁄ _dx ^{3.e^2x}⁄ _1-2x
= 3 . ^d⁄ _dx ^{e^2x}⁄ _1-2x
= 3 . ^{(1 - 2x)
^d⁄
_dx e^2x
- e^2x
^d⁄
_dx (1 - 2x)}⁄ _{(1 - 2x)²}
= 3 . ^{(1 - 2x) e^2x .
^d⁄
_dx 2x
- e^2x (-2)}⁄ _{(1 - 2x)²}
= 3 . ^{(1 - 2x) e^2x . 2
+ 2e^2x}⁄ _{(1 - 2x)²}
= 3 . ^{((1 - 2x).2 + 2) e^2x}⁄ _{(1 - 2x)²}
= 3 . ^{(2 - 4x + 2) e^2x}⁄ _{(1 - 2x)²}
= 3 . ^{(4 - 4x) e^2x}⁄ _{(1 - 2x)²}

Example 9.
Find ^dy⁄_dx .
(a) y = e^x ln x
(b) y = log₁₀ e^x^²
(c) y = log₃(sin x + e^x)
(d) xe^y + ln (xy) = sin x

Solution
(a) y = e^x ln x
^dy⁄_dx = e^x ^d⁄_dx ln x + ln x ^d⁄_dx e^x
= e^x ⋅ ¹⁄_x + ln x ⋅ e^x

(b) y = log₁₀ e^x^² = x² log₁₀ e
log_₁₀ e = 0.4342944819 ဖြစ်သည်။ တနည်းအားဖြင့် constant ပါ။
y = x² log_₁₀ e
^dy⁄ _dx = x² ^d⁄ _dx log_₁₀ e + log_₁₀ e ^d⁄ _dx x²
= x² . 0 + log_₁₀ e . 2x
= log_₁₀ e . 2x

(c) y = log₃(sin x + e^x)
^dy⁄ _dx = ¹⁄ _{(sin x + e^x)} .log_₃ e ^d⁄ _dx (sin x + e^x)
= ¹⁄ _{(sin x + e^x)} .log_₃ e (cos x + e^x)

(d) xe^y + ln (xy) = sin x

Differentiate both sides with respect tox
(x ^d⁄ _dx e^y + e^y ^dx⁄ _dx) + ^d⁄ _dx ln (xy) = ^d⁄ _dx sin x
(x.e^y. ^dy⁄ _dx + e^y.1) + ¹⁄ _xy. ^d⁄ _dx (xy) = cos x
(x.e^y. ^dy⁄ _dx + e^y) + ¹⁄ _xy⋅(x ⋅ ^dy⁄ _dx + y ⋅ ^dx⁄ _dx) = cos x
(x.e^y ⋅ ^dy⁄ _dx + e^y) + ¹⁄ _xy⋅(x⋅ ^dy⁄ _dx + y⋅1) = cos x
x.e^y⋅ ^dy⁄ _dx + e^y + ¹⁄ _xy⋅x ^dy⁄ _dx + ¹⁄ _xy.y = cos x
x.e^y ⋅ ^dy⁄ _dx + e^y + ¹⁄ _y ⋅ ^dy⁄ _dx + ¹⁄ _x = cos x
x.e^y ⋅ ^dy⁄ _dx + ¹⁄ _y. ^dy⁄ _dx = cos x - e^y - ¹⁄ _x
(x.e^y + ¹⁄ _y)⋅ ^dy⁄ _dx = cos x - e^y - ¹⁄ _x
^dy⁄ _dx = ^{cos x - e^y -
¹⁄
_x}⁄ _{x.e^y +
¹⁄
_y}

Example 10.
Differentiate y = x^x, x > 0.
Solution
y = x^x
y = e^{ln x^x}
y = e^{x ln x}
^dy⁄_dx = ^d⁄_dx e^{x ln x}
= e^{x ln x} ^d⁄_dx (x ln x)
= e^{x ln x} (x ⋅ ¹⁄_x + ln x ⋅ 1)
= x^x (1 + ln x)

Exercise 8.4
1. Differentiate the following functions with respect to x.
(a) (5 + 3x)e^-2x

(b) 3^xx³

(c) 2^x log₂ x

(d) 10^x log₁₀(x + 1)

(e) ^{x² + tan 3x}⁄_e^x

(f) x ln y + e^xy = 2

2. Given that y = e^3x sin 2x, prove that ^d²y⁄_dx² - 6 ^dy⁄_dx + 13y = 0.

3. Use logarithmic differentiation to find the derivative of y with respect to x.
$$ \small{\text{(a)} \,\, y = (\sqrt{x})^x } $$
(b) y = x^{cos x}

(c) y = (ln x)^{ln x}