Chapter 7
Trigonometric Functions
7.1 Graphs of Sine Functions
Graph of the Sine Function y = sin x
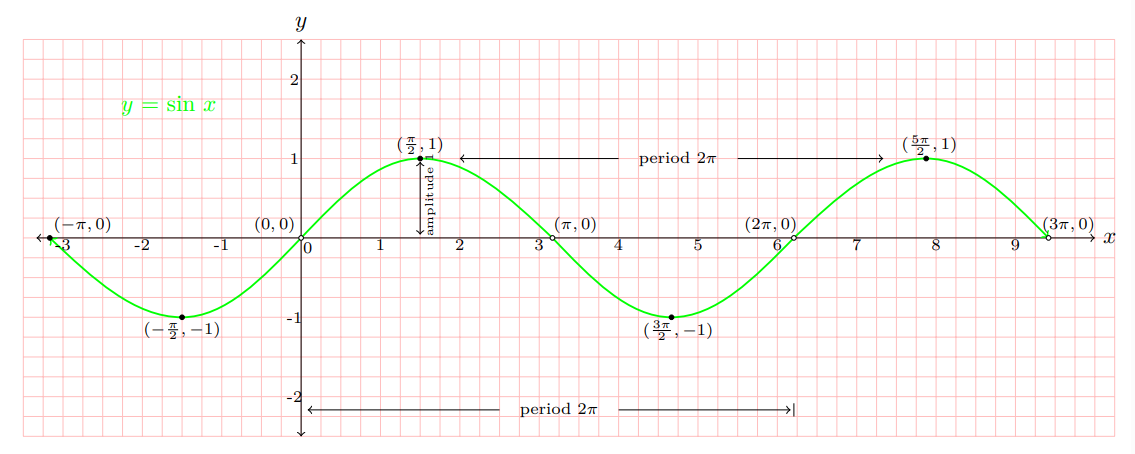
Domain: The set ℝ of all real numbers. Range: {y| -1 ≤ y ≤ 1}
$$\scriptsize{ \text{Five key points:} \begin{cases}x\text{-intercepts:} (0,0), (\pi ,0) (2\pi , 0)\\ \text{maximum point:} (\dfrac{\pi}{2},1) \quad \text{minimum point:}
(\dfrac{3\pi}{2},-1) \end{cases} } \,$$
Periodic function: If f(x) = f(x + p) where p is a positive real number, then the function F is called a periodic function.
If p is the smallest such number, then p is the period of function f. The sine function y = sin x is a periodic function
with period 2π, since 2π is the smallest positive real number such that sin x = sin (x + 2x).
The amplitude of a periodic function is half the difference between the maximum and the minimum values. So the amplitude of the sine function
y = sin x is
1 - (-1)⁄2 = 1.Graph of the Sine Function y = a sin bx, a > 0, b > 0
In the following example, we will see how to obtain the graph of y = a sin bx, where a > 0 and b > 0, from the graph of y = sin x.Example 1.
From the graph of y = sin x, draw step-by-step transformation graph to get the graph of y = 2 sin π⁄2 x.
Solution
Method 1
$$y = \text{sin}\, x \xrightarrow[\text{scale factor 2}] {\text{vertical scaling}} \, y = \text{2 sin}\, x $$
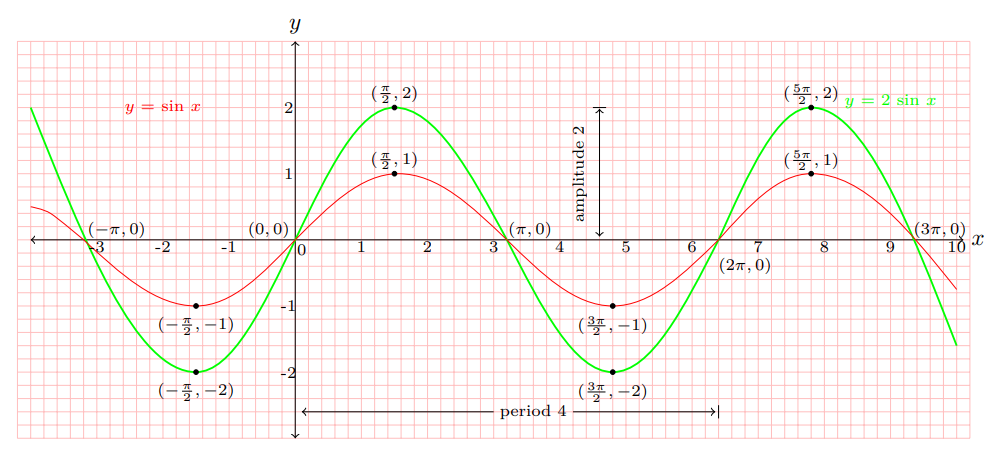
$$y = \text{sin}\, x \, \xrightarrow[\text{scale factor 2}]{\text{vertical scaling}} \, y = \text{2\, sin} \, x \,
\xrightarrow[\text{scale factor}\, \tiny{\dfrac{1}{\dfrac{\pi}{2}} = \dfrac{2}{\pi} }]{\text{horizontal scaling}} y = \text{2 sin}
\dfrac{\pi}{2} x \, $$
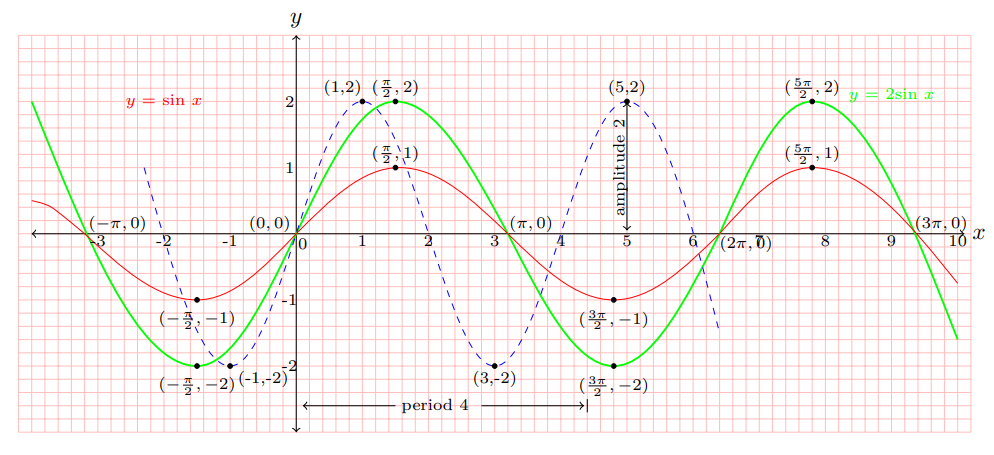
Method 2
$$y = \text{sin}\, x \, \xrightarrow[\text{scale factor}\, \tiny{\dfrac{1}{\dfrac{\pi}{2}} = \dfrac{2}{\pi} }]{\text{horizontal scaling}} y = \text{sin} \dfrac{\pi}{2} x $$
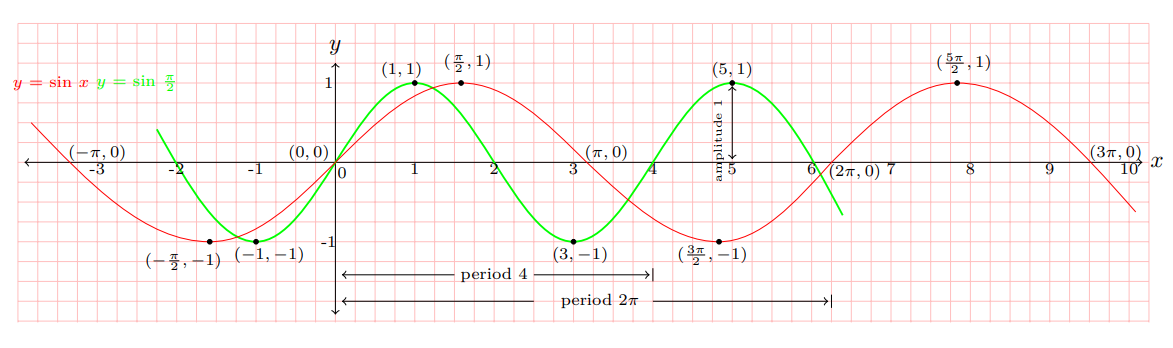
$$y = \text{sin}\, x \, \xrightarrow[\text{scale factor}\, \tiny{\dfrac{1}{\dfrac{\pi}{2}} = \dfrac{2}{\pi} }]{\text{horizontal scaling}} y =
\text{sin}\, \dfrac{\pi}{2} \, x =
\xrightarrow[\text{scale factor 2}]{\text{vertical scaling}} \, \text{2 sin}
\dfrac{\pi}{2} x \,$$
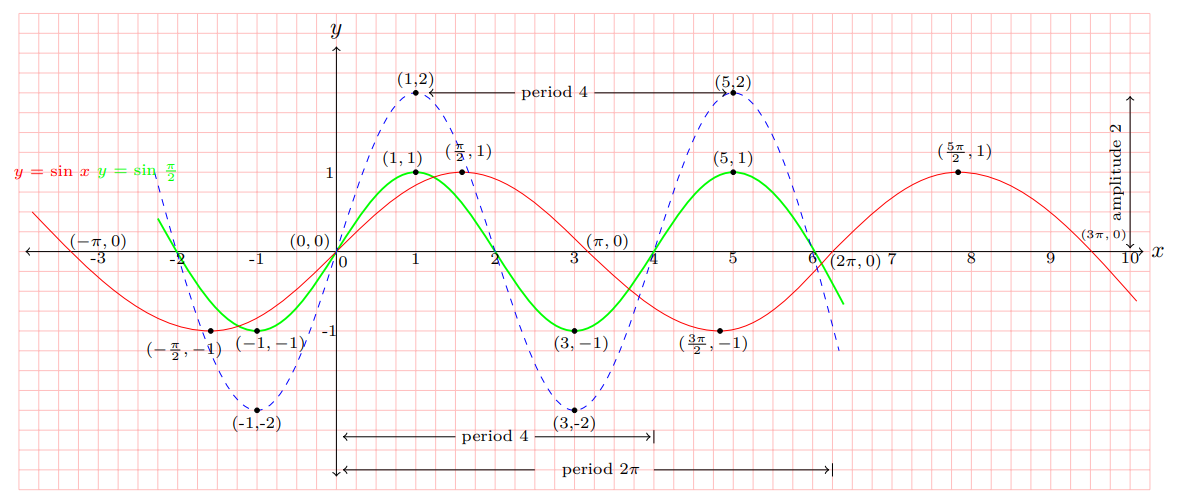
From the graph of y = sin x, the graph of y = a sin bx, a > 0, b > 0, can be obtained as
$$y = \text{sin}\, x \, \xrightarrow[\text{scale factor }a]{\text{vertical scaling}} \, y = a\, \text{sin} \, x \,
\xrightarrow[\text{scale factor}\, \tiny{\dfrac{1}{b}} ] {\text{horizontal scaling}}
y = a\, \text{sin} \,
bx \, \, $$
or
$$y = \text{sin}\, x \, \xrightarrow[\text{scale factor}\, \tiny{\dfrac{1}{b}} ] {\text{horizontal scaling}} \, y = \text{sin} \, bx \,
\xrightarrow[\text{scale factor }a]{\text{vertical scaling}}
y = a\, \text{sin} \,
bx \, $$
y = sin x → y = a sin bx
(x,y) → (x⁄b, ay)
(x,y) → (x⁄b, ay)
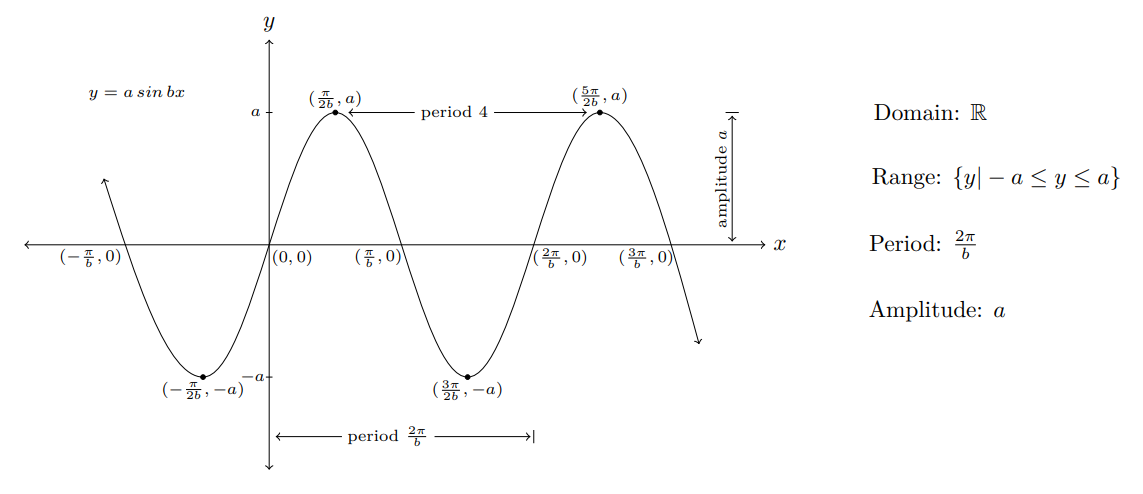
$$\scriptsize{ \text{Five key points:} \begin{cases}x\text{-intercepts:} (0,0), (\dfrac{\pi}{b} ,0), (\dfrac{2\pi}{b} , 0)\\ \text{maximum point:} (\dfrac{\pi}{2b},a) \quad \text{minimum point:}
(\dfrac{3\pi}{2b},-a) \end{cases} } \,$$
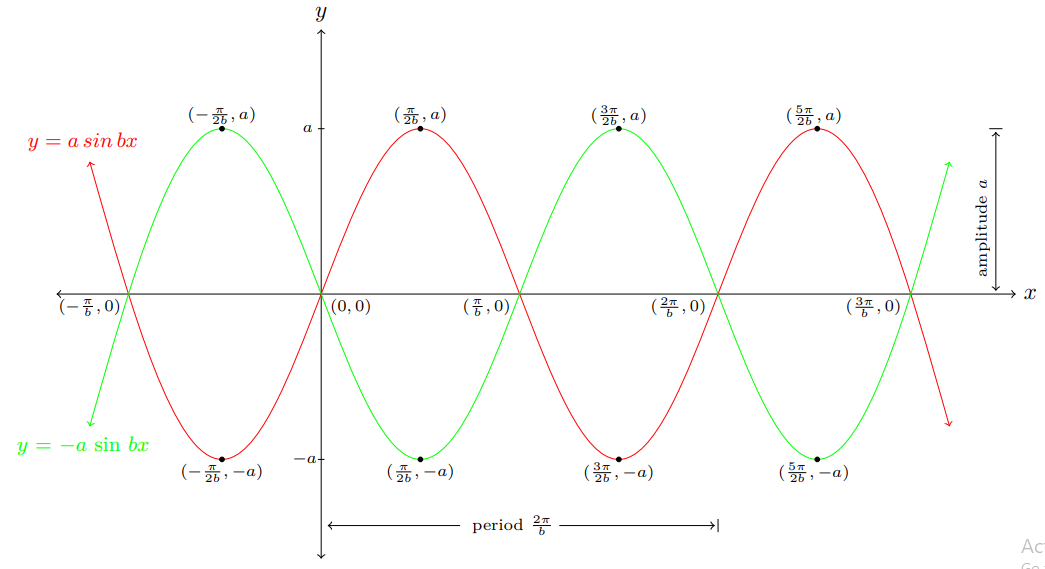
Graph of the Sine Function y = -a sin bx, a > 0, b > 0
$$y = a\, \text{sin}\, bx\, \xrightarrow{\text{Reflection on the}\, x\text{-axis}}\, y = -a\, \text{sin}\, bx \,$$
Example 2
Draw the graph of y = 2 sin π⁄2 x and y = -2 sin π⁄2 x.
Solution
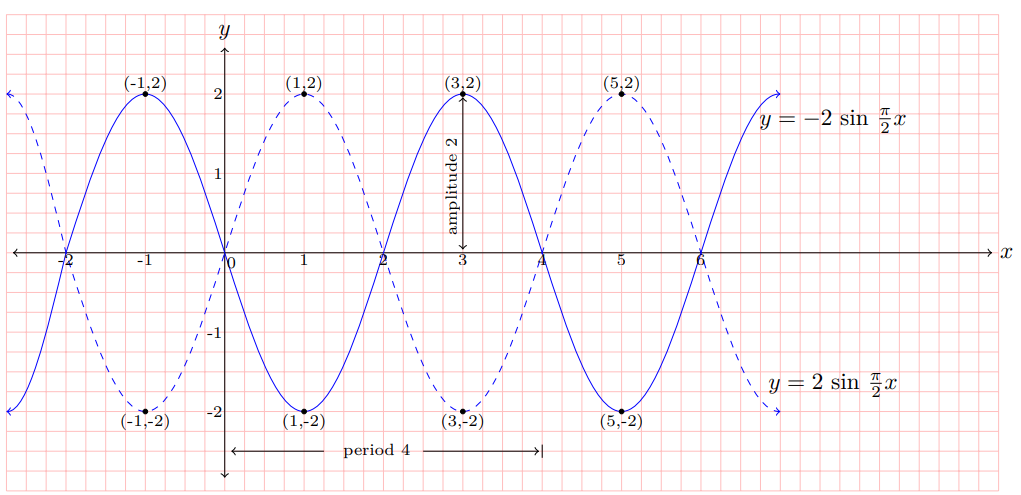
Note that y = a sin (-b)x = -a sin bx, so no need to consider b < 0.
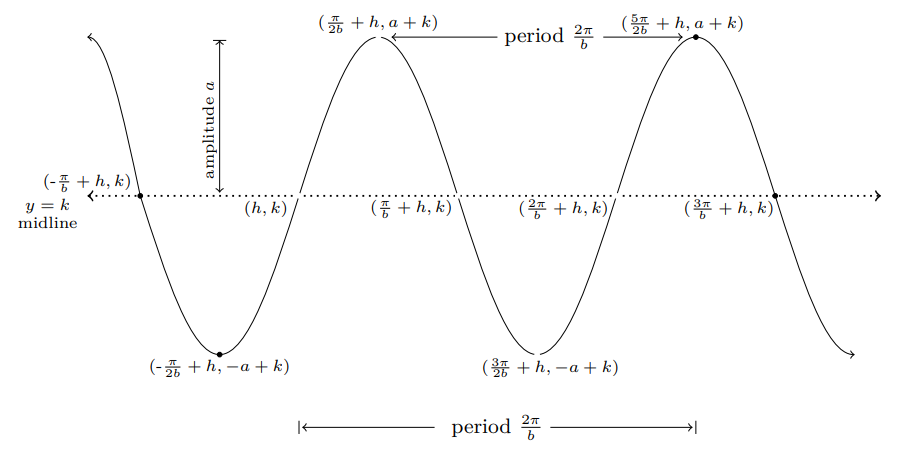
Graph of the Sine Function y = a sin b(x - h) + k
$$\small{y = a \, \text{sin}\, bx\, \xrightarrow[\text{vertical translation}\, k\, \text{units}] {\text{horizontal translation}\, h\, \text{units}} \, y}$$
$$\small{= a \, \text{sin} \, b(x - h) + k }$$
y = sin x → y = a sin bx → y = a sin b(x - h) + k
(x, y) → (x⁄b, ay) → ( x⁄b + h, ay + k)
(x, y) → (x⁄b, ay) → ( x⁄b + h, ay + k)
Key points on the midline y = k
- (0,0) → (0, 0) → (h, k)
- (π, 0) → (π⁄b, 0) → (π⁄b + h, k)
- (2π, 0) → (2π⁄b, 0) → (2π⁄b+h, k)
Maximum and minimum points
- (π⁄2,1) → (π⁄2b, a) → (π⁄2b+h, a+k)
- (3π⁄2, -1) → (3π⁄2b, -a) → (3π⁄2b+h, -a+k)
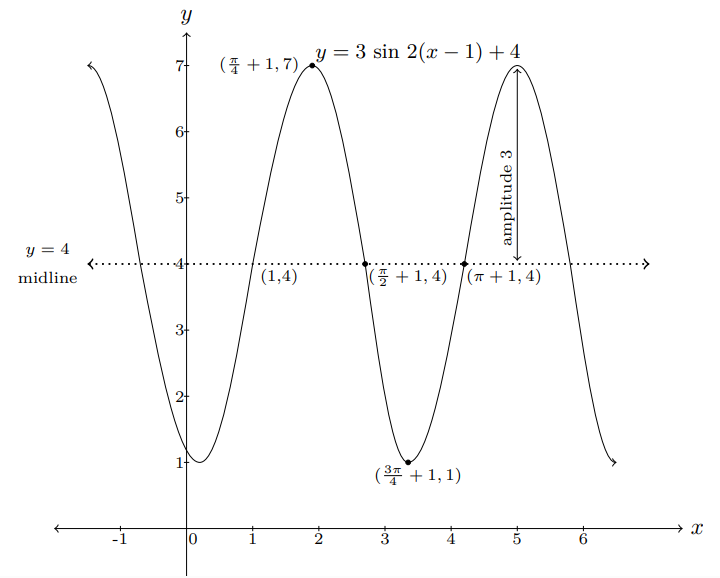
Example 3.
Draw the graph of y = 3 sin 2 (x - 1) + 4.
Solution
Midline: y = 4,
Amplitude: 3,
Period: π
Five key points: (1, 4), (π⁄4+1, 7), (π⁄2+1, 4), (3π⁄4+1, 1), (π+1, 4)
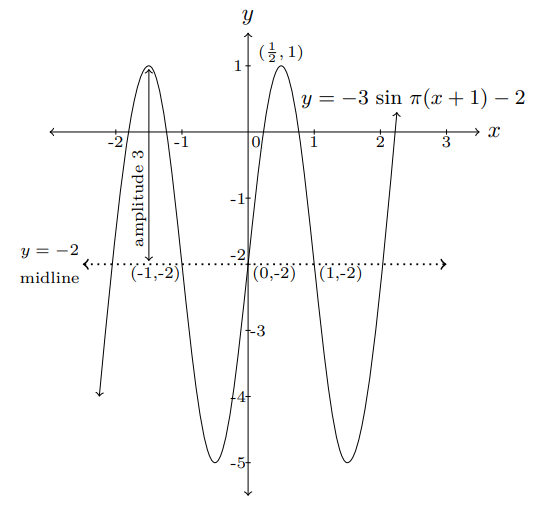
Example 4.
Draw the graph of y = -3 sin π(x + 1) - 2.
Solution
Midline: y = -2,
Amplitude: 3,
Period: 2
Five key points: (-1, -2), (- 1⁄2, -5), (0, -2), (1⁄2, 1), (1, -2)
1. From the graph of y = sin x, draw step-by-step transformation graphs to get the graph of y = -3 sin π⁄3 x.
2. Draw the graph of (a) y = 1⁄2 sin x
(b) y = sin 4x.
3. Draw the graph of (a) y = 2 sin π⁄4 x
(b) y = -sin πx.
4. Draw the graph of (a) y = 2 sin π⁄3(x-2) + 1
(b) y = -2 sin 1⁄2(x+1) + 2.
5. Show that y = a sin bx is an odd function.
7.2 Graphs of Cosine Functions
Graph of the Coine Function y = cos x
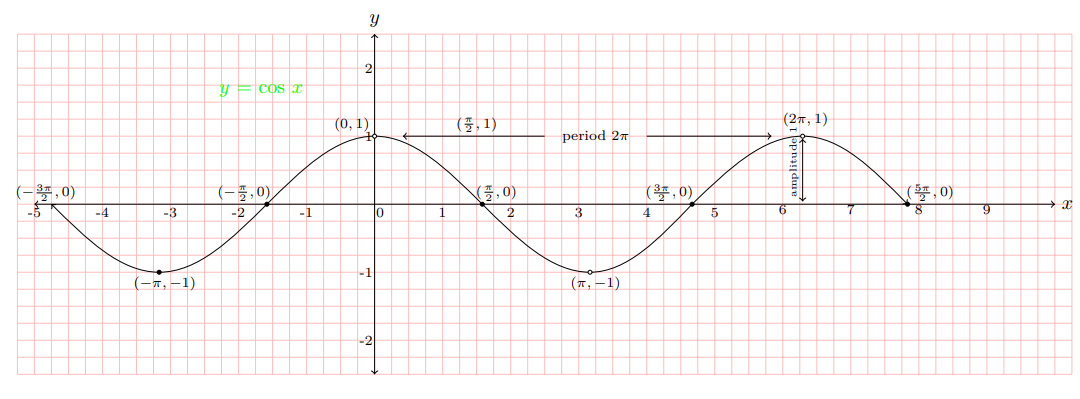
Domain: The set ℝ of all real numbers. Range: {y| -1 ≤ y ≤ 1}
$$\scriptsize{ \text{Five key points:} \begin{cases}x\text{-intercepts:} (\dfrac{\pi}{2},0), (\dfrac{3\pi}{2} , 0)\\ \text{maximum point:} (0,1), (2\pi, 1) \quad \text{minimum point:}
(\pi,-1) \end{cases} } $$
$$\text{Note\ that\ sin} (x + \dfrac{\pi}{2}) = cos \ x ,$$
$$y = \text{sin}\, x \xrightarrow[- \dfrac{\pi}{2} \, \text{units}] {\text{horizontal translation}} \, y = \text{cos}\, x $$
Graph of the Cosine Function y = a cos bx, a > 0, b > 0
From the graph of y = cos x, the graph of y = a cos bx can be obtained as
$$\scriptsize{y = a \, \text{sin}\, bx\, \xrightarrow[\text{horizontal scaling, scale factor}\, \tiny{\dfrac{1}{b}}] {\text{vertical scaling, scale factor}\, a} \, y = a
\, \text{cos}\, bx}$$
$$\scriptsize{(x,y) \rarr \, (\dfrac{x}{b}, ay) }$$
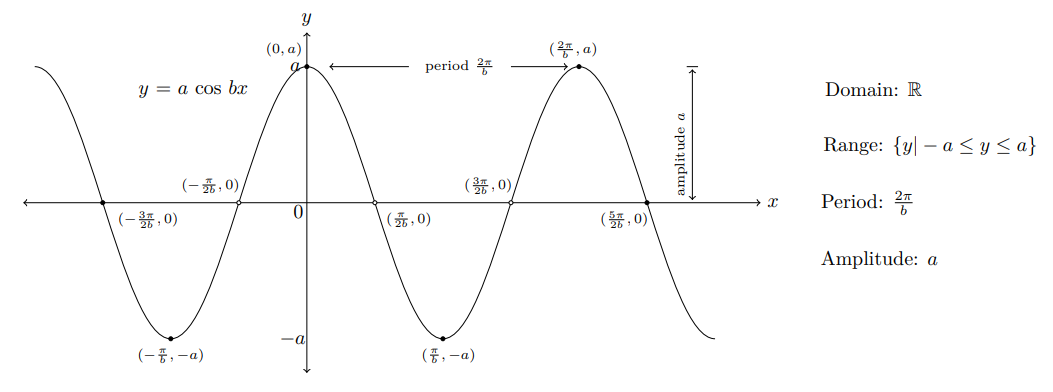
$$\scriptsize{ \text{Five key points:} \begin{cases}x\text{-intercepts:} (\dfrac{\pi}{2b},0), (\dfrac{3\pi}{2b} , 0)\\ \text{maximum point:} (0,a),
(\dfrac{2\pi}{b}, a) \quad \text{minimum point:} (\dfrac{\pi}{b},-a) \end{cases} } $$
Graph of the Cosine Function y = -a cos bx, a > 0, b > 0
$$y = a\, \text{cos}\, bx\, \xrightarrow{\text{Reflection on the}\, x\text{-axis}}\, y = -a\, \text{cos}\, bx $$
Example 5.
Draw the graphs of y = 1⁄2 cos 2x and y = - 1⁄2 cos 2x
Solution
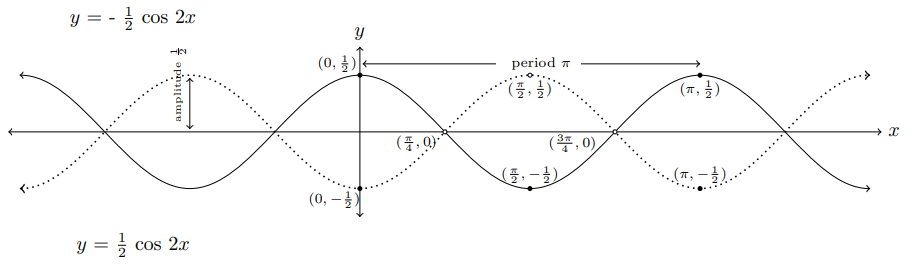
Note that y = a cos (-b)x = a cos bx, so no need to consider b < 0.
Graph of the Cosine Function y = a cos b(x - h) + k , a > 0, b > 0
$$\small{y = a \, \text{cos}\, bx\, \xrightarrow[\text{vertical translation}\, k\, \text{units}] {\text{horizontal translation}\, h\, \text{units}} \, y}$$
$$\small{= a \, \text{cos} \, b(x - h) + k }$$
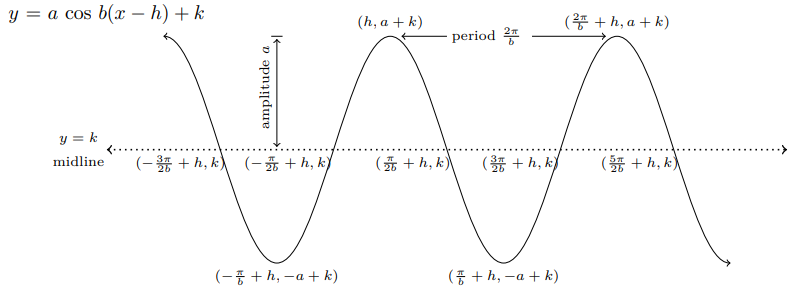
y = cos x → y = a cos bx → y = a cos b(x - h) + k
(x, y) → (x⁄b, ay) → ( x⁄b + h, ay + k)
(x, y) → (x⁄b, ay) → ( x⁄b + h, ay + k)
Five key points: points on the midline : (π⁄2b + h, k), (3π⁄2b + h, k)
maximum points: (h, a + k), (2π⁄b + h, a+k) minimum point: (π⁄b + h, -a+k)
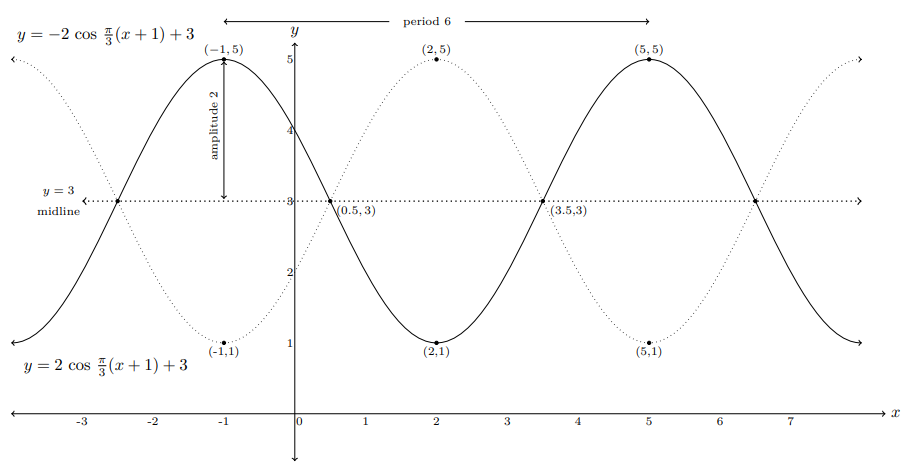
Example 6.
Draw the graph of y = 2 cos π⁄3 (x + 1) + 3 and y = -2 cos π⁄3 (x + 1) + 3.
Solution
Midline: y = 3,
Amplitude: 2,
Period: 6
Five key points for y = 2 cos π⁄3 (x + 1) + 3: (-1, 5), (0.5, 3), (2, 1), (3.5, 3), (5, 5)
Five key points for y = - 2 cos π⁄3(x + 1) + 3: (-1, 1), (0.5, 3), (2, 5), (3.5, 3), (5, 1)
Exercise 7.2
1. From the graph of y = cos x, draw step-by-step transformation graphs to get the graph of y = -3 cos π⁄2 x.
2. Draw the graph of (a) y = 1⁄2 cos x
(b) y = cos 4x.
3. Draw the graph of (a) y = 2 cos π⁄4 x
(b) y = -sin πx.
4. Draw the graph of (a) y = 2 cos π(x-2) + 1
(b) y = -2 cos 1⁄2(x+1) + 2.
5. Show that y = cos bx is an even function.
7.3 Graphs of Other Trigonometric Functions
Graph of y = 10 x and y = cot x
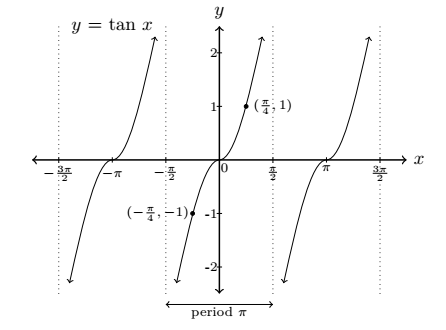
Domain: x ≠ ± π⁄2, ± 3π⁄2, ...
Range: ℝ
Period: π
x-intercepts: x = 0, ±&pi, ±2π, ...
Asymptotes: x = ±π⁄2, ± 3π⁄2, ...
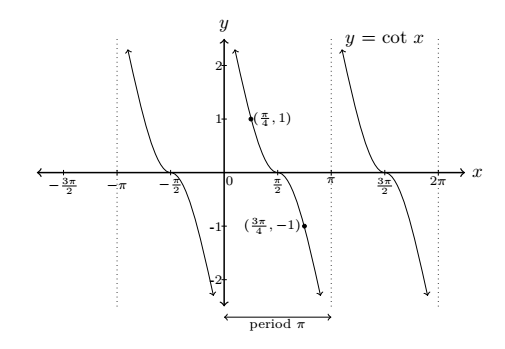
Domain: x ≠ 0, ±π, ±2π, ...
Range: ℝ Period: π
x-intercepts: x = ±π⁄2, ± 3π⁄2, ...
Asymptotes: x = 0, ±π, ±2π, ...
Example 7.
Draw the graphs of y = a tan bx and y = a cot bx for a, b > 0.
Solution
y = tan x → y = a tan bx,
(x, y) → (x ⁄b, ay)
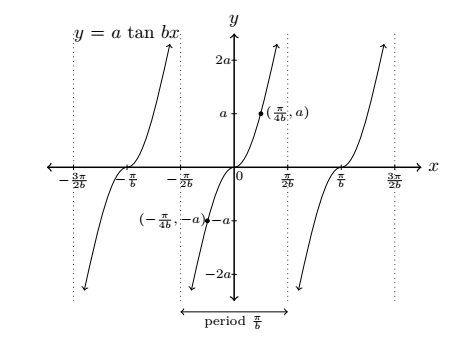
y = cot x → y = a cot bx
(x, y) → (x ⁄b, ay)
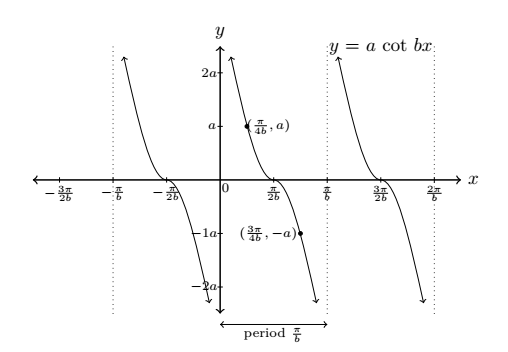
Graph of y = sec x and y = csc x
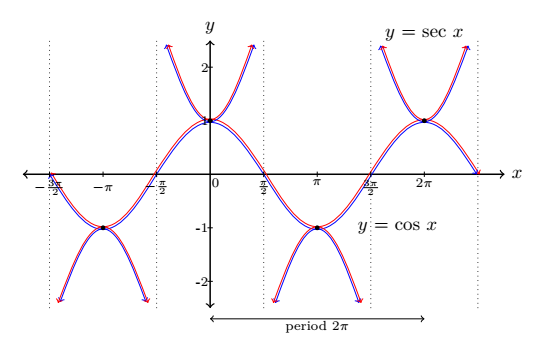
Domain: x ≠ ± π⁄2, ± 3π⁄2, ...
Range: y ≤ -1 or y ≥ 1
Period: 2π
x-intercepts: x = 0, ±π, ±2π, ...
Asymptotes: x = ±π⁄2, ± 3π⁄2, ...
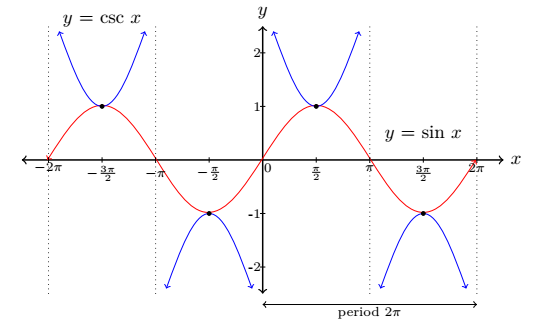
Domain: x ≠ 0, ±π, ±2π, ...
Range: y ≤ -1 or y ≥ 1
Period: 2π
x-intercepts: x = ±π⁄2, ± 3π⁄2, ...
Asymptotes: x = 0, ±π, ±2π, ...
Note that transform y = sec x to y = a sec bx and y = csc x to y = a csc bx with (x, y) → (x⁄b, ay), we get the graph of y = a sec bx and y = a csc bx.
Exercise 7.3
1. Draw the graph of (a) y =
1⁄2 tan πx
(b) y = 2 tan
1⁄2 x.
2. Draw the graph of (a) y = 2 cot
π⁄3 x
(b) y = 3 cot 2x.
3. Draw the graph of (a) y = 2 sec πx
(b) y = 2 csc 1⁄2 x.
4. Show that y = a tan bx , y = a cot bx, and y = a csc bx are odd functions.
5. Show that y = a sec bx is an even function.
7.4 Inverse Trigonometric Functions
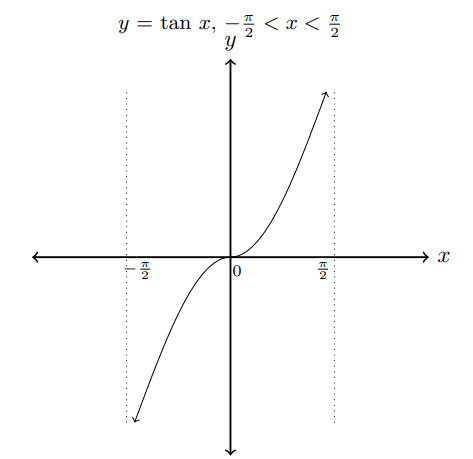
Trigonometric functions are not one-to-one functions. So we need to restrict the domain of each function to be a one-to-one function to get the inverse trigonometric functions. The following graphs shows that y = sin x, y = cos x, and y = tan x are one-to-one in the restricted domains.In these restricted domains, we can define the inverse functions y = sin-1x, y = cos-1x and y = tan-1x.
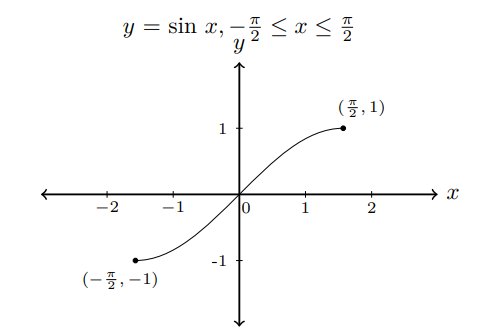
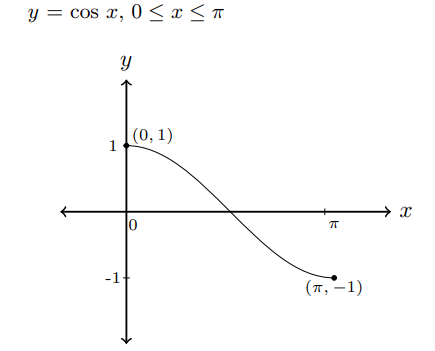
- y = sin-1x if sin y = x for -1 ≤ x ≤ 1, - π⁄2 ≤ y ≤ π⁄2
- y = cos-1 x if cos y = x for -1 ≤ x ≤ 1, 0 ≤ y ≤ π
- y = tan-1 x if tan y = x for x ∈ R
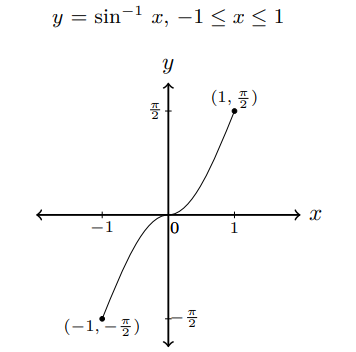
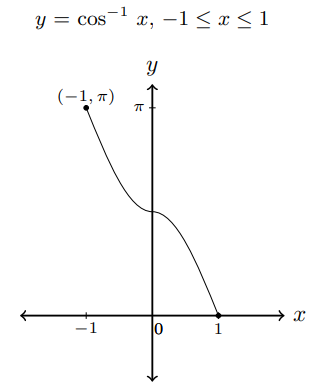
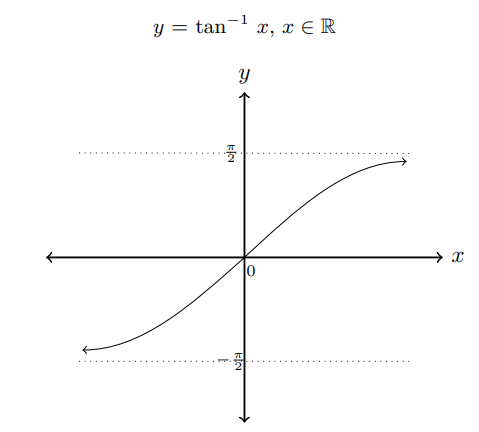
We can define the other trigonometric functions in the same manner.
- y = cot -1x if cot y = x for x ∈ R, 0 < y < π
- y = sec-1 x if sec y = x for |x| ≥ 1, 0 ≤ y ≤ π, y ≠ π⁄2
- y = csc-1 x if csc y = x for |x| ≥ 1, - π⁄2 ≤ y ≤ π⁄2, y ≠ 0
Example 8.
Evaluate (a) sin-1 1⁄2
(b) cos-1 - (1⁄2)
$$\small{\text{(c) tan}^{-1} (-\sqrt{3})}$$ (d) sin-1 (sin 5π⁄6 ).
Solution
(a) Since sin π⁄6 = 1⁄2 and - π⁄2 ≤ π⁄6 ≤ π⁄2,
we have sin-1 1⁄2 = π⁄6.
(b) Since cos 2π⁄3 = - 1⁄2 and
0 ≤ 2π⁄3 ≤ π, we have
cos-1 (- 1⁄2) = 2π⁄3.
(c) Since tan(- π⁄3) = - √ 3 and
- π⁄2 ≤ - π⁄3 ≤ π⁄2, we have
tan-1 (- √ 3 ) = - π⁄3.
(d) sin-1(sin 5π⁄6) = sin-1 (1⁄2) = π⁄6.
From y = sin-1 x if sin y = x, we have sin(sin-1 x) = x for the domain -1 ≤ x ≤ 1 of y = sin-1 x, but from Example 8(d) one can see that
sin-1(sin x) = x is not true in general.
Since sin(-sin-1x) = -sin(sin-1x) = -x, we have
sin-1(-x) = -sin-1x
so y = sin-1x is an odd function.
From y = cos-1x if cos y = x, we have cos(cos-1x) = x for the domain -1 ≤ x ≤ 1 of y = cos-1x. Since cos(π - cos-1x) = - cos(cos-1x) = -x,
π - cos-1x = cos-1(-x)
or
cos-1x + cos-1(-x) = π
1. Evaluate (a) csc(sin-10.3)
(b) cot(tan-1 5)
(c) sec(cos-1(-0.75)).
2. Evaluate (a) sin-1 √ 3 ⁄2
(b) cos-1 √ 2 ⁄2
(c) tan-1 √ 3 ⁄3
3. Evaluate (a) sin(cos-1 √ 3 ⁄2 )
(b) tan(sin-1 √ 3 ⁄2)
(c) csc(tan-1(- √ 3 ⁄3 ))
4. Evaluate (a) sin-1(sin 2π⁄3)
(b) cos-1(cos(- 1⁄2))
(c) tan-1(tan(- √ 3 ))
5. Prove that sin-1 x + cos-1 x = π⁄2
7.5 Differentiation of Trigonometric Functions
Before we study the differentiation of trigonometric functions, we first evaluate an important limit, $$\small{\lim_{x\to 0} \frac{sin\, x}{x}.} $$Consider the unit circle in the following figure with radii OA and OB with OA = OB = 1 and ∠AOB = x radians.
Obviously, BD < arc AB < AC. In right ▵OBD, BD = OB sin x = sin x.
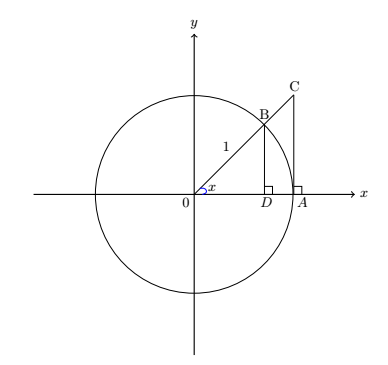
In right ∆OAC, AC = OA tan x = tan x.
Length of arc AB = OB ⋅ x = x, we have
sin x < x < tan x
sin x⁄sin x < x⁄sin x < tan x⁄sin x
1 < x⁄sin x < 1⁄cos x
1 > sin x⁄x > cos x
When x → 0, cos x → 1.
$$\small{ \text{Since}\, \lim_{x\to 0}1 = 1 \, \text{and} \, \lim_{x\to0}\, cos \, x\, = \, 1, } $$ $$\small{ \lim_{x\to0} \frac{sin \, x}{x} = 1 } $$ Derivative of sin x
Let y = sin x.
y + δy = sin(x + δx)
∴ δy = sin(x + δx) - sin x
= 2 cos(x + δx⁄2) ⋅ sin δx⁄2 (sin α - sin β = 2cos α + β⁄2 ⋅ sin α - β⁄2)
$$\small{ \frac{dy}{dx} = \lim_{\delta x\to0} \frac{\delta y}{\delta x} } $$ $$\small{ = \lim_{\delta x\to0} \frac{2 \text{cos}(x + \frac{\delta x}{2})\, \sdot\, \text{sin} \frac{\delta x}{2}} {\delta x} }$$ $$\small{= \lim_{\delta x\to0} \text{cos}(x + \frac{\delta x}{2})\, \sdot\, \lim_{\delta x\to0} \frac{\text{sin} \frac{\delta x}{2}}{\frac{\delta x}{2}} }$$ = cos x × 1 (when δx→ 0, δx⁄2 → 0)
d⁄dx sin x = cos x
In general,
d⁄dx sin u(x) = cos u(x) ⋅ d⁄dx u(x).
Derivative of cos x
Since cos x = sin(π⁄2 + x)
d⁄dx cos x = d⁄dx sin(π⁄2 + x)
= cos(π⁄2 + x) ⋅ d⁄dx(π⁄2 + x)
= - sin x × 1 (∵ cos(π⁄2 + x) = - sin x)
d⁄dx cos x = - sin x
In general,
d⁄dx cos u(x) = - sin u(x) ⋅ d⁄dx u(x).
Derivative of tan x
Since tan x = sin x⁄cos x
d⁄dx tan x = d⁄dx sin x⁄cos x
= cos x ⋅ d⁄dx sin x - sin x ⋅ d⁄dx cos x ⁄cos2 x
= cos x ⋅ cos x - sin x ⋅ (- sin x)⁄cos2x (quotient formula)
cos2 x + sin2 x⁄cos2 x
= 1 ⁄cos2 x (cos2 x + sin2 x = 1)
= sec2 x (sec x = 1 ⁄cos x)
∴ d⁄dx tan x = sec2 x
In general,
d⁄dx tan u(x) = sec2 u(x) ⋅ d⁄dx u(x).
Similarly, we can easily find the formulas for the derivatives of cot x, sec x and csc x.
Formulas for derivatives of trigonometric functions
| 1 | d⁄dx sin (x) = cos x , | d⁄dx sin u(x) = cos u(x). d⁄dx u(x). |
| 2 | d⁄dx cos (x) = -sin x , | d⁄dx cos u(x) = -sin u(x). d⁄dx u(x). |
| 3 | d⁄dx tan (x) = sec2 x , | d⁄dx tan u(x) = sec2 u(x). d⁄dx u(x). |
| 4 | d⁄dx cot (x) = -cosec2 x , | d⁄dx cot u(x) = -cosec2 u(x). d⁄dx u(x). |
| 5 | d⁄dx sec (x) = sec x. tan x , | d⁄dx sec u(x) = sec u(x). tan u(x). d⁄dx u(x). |
| 6 | d⁄dx csc (x) = -csc x. cot x , | d⁄dx csc u(x) = -csc u(x). cot u(x). d⁄dx u(x). |
Differentiate the following functions with respect to x.
(a) sin 5x
(b) cos (7x2 - 2)
(c) tan(6x + 7)
(d) 5 sec(3x + 1)
(e) cot(1 - 2x)⁄3
(f) -2 csc 3x
Solution
(a) d⁄dx sin 5x = cos 5x ⋅ d⁄dx 5x
= cos 5x ⋅ 5 = 5 cos 5x
(b) d⁄dx cos (7x2 - 2) = - sin(7x2 - 2) ⋅ d⁄dx (7x2 - 2)
= - sin (7x2 - 2) ⋅ 14x
(c) d⁄dx tan(6x + 7) = sec2(6x + 7) ⋅ d⁄dx (6x + 7)
= sec2 (6x + 7) ⋅ 6
(d) d⁄dx 5 sec(3x + 1) = 5⋅ sec(3x + 1) ⋅ tan(3x + 1) ⋅ d⁄dx (3x + 1)
= 5⋅ sec(3x + 1) ⋅ tan(3x + 1) ⋅ 3
= 15 ⋅ sec(3x + 1) ⋅ tan(3x + 1)
(e) d⁄dx cot(1 - 2x)⁄3 = 1⁄3 ⋅ d⁄dx cot(1 - 2x)
= 1⁄3 ⋅ - csc2(1 - 2x) ⋅ d⁄dx (1 - 2x)
= - 1⁄3 ⋅ csc2(1 - 2x) ⋅ (-2)
= 2⁄3 ⋅ csc2(1 - 2x)
(f) d⁄dx (-2 csc 3x) = -2 (-csc 3x ⋅ cot 3x) ⋅ d⁄dx 3x
= 2 csc 3x ⋅ cot 3x ⋅ 3
= 6 csc 3x ⋅ cot 3x
Example 10.
Find dy⁄dx.
(a) y = sin2 x
(b) y = cos √ x
(c) y = tan2 (x2)
(d) y = sin 2x - x cos x
(e) y = sin x ⋅ cos2 x
(f) y = x ⁄tan x
(g) y = √ x + 10x
Solution
(a) y = sin2 x
dy⁄dx = d⁄dx sin2x
= 2 sin x d⁄dx sin x
= 2 sin x cos x
(b) y = cos √ x
dy⁄dx = d⁄dx cos √ x
= - sin √ x d⁄dx x1⁄2 = - sin √ x ⋅ 1⁄2 x ( 1⁄2 - 1)
= - sin √ x ⋅ 1⁄2 x( - 1⁄2)
(c) y = tan2 (x2)
dy⁄dx = 2 tan (x2) d⁄dx tan (x2)
= 2 tan (x2).sec2 (x2) dy⁄dx x2
= 2 tan (x2).sec2 (x2).2x
(d) y = sin 2x - x cos x
dy⁄dx = cos 2x. d⁄dx 2x - [x.d⁄dx cos x + cos x dx⁄dx ]
= 2 cos 2x - [x (-sin x) + cos x.1]
= 2 cos 2x + x sin x - cos x
(e) y = sin x.cos2 x
dy⁄dx = sin x. d⁄dx (cos2 x) + cos2 x. d⁄dx (sin x)
= sin x.2 cos x. d⁄dx (cos x) + cos2 x.cos x
= sin x. 2 cos x.(-sin x) + cos2 x. cos x
= -2 sin2 x.cos x + cos3 x
(f) y = x⁄3 tan x
dy⁄dx = tan x. dx⁄dx - x. d⁄dx tan x ⁄(tan x)2
= tan x.1 - x sec2 x ⁄tan2 x
= tan x - x sec2 x ⁄tan2 x
(g) y = √ x + sin x = (x + sin x)1/2
dy⁄dx = 1⁄2 (x + sin x)-1/2 . d⁄dx (x + sin x)
= 1⁄2 (x + sin x)-1/2 . (1 + cos x)
= 1 + cos x⁄ 2 √ x + sin x
Example 11.
Given that x + sin y = cos(xy) , find dy⁄dx .
Solution
x + sin y = cos(xy) , find dy⁄dx .
Differentiate with respect to x,
1 + cos y ⋅ dy⁄dx = -sin xy ⋅ d⁄dx (xy)
1 + cos y. dy⁄dx = -x sin (xy). dy⁄dx - y sin (xy)
x sin (xy). dy⁄dx + cos y. dy⁄dx = -y sin xy - 1
(x sin (xy) + cos y). dy⁄dx = -y sin xy -1
dy⁄dx = -y sin xy -1⁄ x sin (xy) + cos y
dy⁄dx = - 1 + y sin xy ⁄ cos y + x sin (xy)
Example 12.
Given that y = x sin x, find d2y ⁄dx2.
Solution
y = x sin x
dy⁄dx = x d⁄dx sin x + sin x.
dx⁄dx = x.cos x + sin x
d2y⁄ dx2 = (x⋅d⁄dx cos x + cos x ⋅ dx⁄dx ) + d⁄dx sin x
= x (-sin x) + cos x + cos x
= 2 cos x - x sin x
Exercise 7.5
1. Differentiate the following function with respect to x.
(a) sin (2x + 3),
(b) cos 3⁄x
(c) x3 cos 2x ,
(d) cos 7x + sin 3x
(e) sin x.cos 2x,
(f) cos2 (5x)
(g) tan3 √ x ,
(h) sin (cos x)
(i) sin x⁄ 1 + tan x ,
(j) √ sin x + cos x
2. Find dy⁄dx.
(a) y = sin (1 - x2) ,
(b) y = 2 π x + 2 cos π x.
(c) y = sin2 x . cos 3x ,
(d) y = x2 sin( 1⁄x)
(e) 3x2 + 2 sin y = y2 ,
(f) sin x . cos y = 2y.
3. Given that y = cos2 x, prove that d2y⁄ dx2 + 4y = 2.
4. Given that y = 1⁄3 cos3x - cos x, prove that dy⁄dx = sin3x.